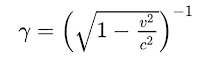The standard Big Bang hypothesis is probably too bold an assumption: a tower of turtles

The Big Bang hypothesis was born when Alexander Friedmann in 1922 found a very nice and simple solution for the Einstein field equations. The solution assumes that the universe topologically differs from Minkowski space. The spatial extent of the universe is like the surface of a balloon which is inflated and expands.

https://en.wikipedia.org/wiki/Friedmann_equations

Our own work in the past two months and earlier makes the concept of curved spacetime suspect  –  it may be impossible to describe gravity through a "metric". We thus exposed a weak point in various Big Bang models: they assume that spacetime is curved, and in addition to that, that spacetime even differs topologically from the familiar flat Minkowski space that we know.

Let us analyze these assumptions.

An interaction is expected to bend light – that does not prove that spacetime itself is curved

Bending of light when it passes the Sun is not a surprise at all. We expect gravity to pull photons. More surprising is that the bending is double the newtonian expectation. It is due to the radial metric stretching.

We have in this blog presented arguments for that the inertia, which a gravity field imposes on a test mass, explains both the slowing down of the time and the stretching of the radial metric close to a mass M. The interaction field can carry energy. One would expect that the field imposes inertia on a test mass m. It is not a surprise at all.

Why would we then assume that spacetime is curved? That is a bold and unnecessary assumption for a very mundane process of an interaction.

We have argued that the electric field expresses phenomena which are similar to gravity. Why would these phenomena in gravity be fundamentally different, so that they show that "spacetime is curved"?

Claiming that the Big Bang is the starting point of the entire universe breaks the Copernican principle

In astronomy we have observed that we live inside an explosion cloud which is expanding. The entire observable universe seems to be inside this explosion cloud.

There are explosions of various sizes in the observable universe, for example, supernova explosions.

Why should we assume that our explosion cloud is the entire universe and that the universe started from that explosion? That is an unnecessary assumption. It breaks the Copernican principle that we should not assume that we are located in a special place and time in the universe. The standard Big Bang model claims that quite a short time, only 13.7 billion years has passed since the beginning of the entire universe. We are special in the standard Big Bang model.

https://en.wikipedia.org/wiki/Friedmann%E2%80%93Lema%C3%AEtre%E2%80%93Robertson%E2%80%93Walker_metric

The Friedmann (FLRW) Big Bang model is very similar to a newtonian expansion of a dust ball. This suggests that we actually live inside an ordinary newtonian explosion. Why should we assume a topologically strange model to explain a simple newtonian explosion?

If we would be free to design the birth of a universe, why should it be so similar to an ordinary newtonian explosion? We could have a fundamentally different mechanism which creates the universe. Why pick a newtonian explosion?

Why the observable universe seems to be spatially flat?

If we use the Friedmann model, we have to fine-tune the mass-energy density of the universe at the early stage, to ensure that the spatial metric is flat after 13.7 billion years. A slight change of the density can make the universe to collapse very quickly.

People devised the inflation model to explain this fine-tuning. The inflation model is very speculative. There should be very good evidence for it before we can accept it.

A simpler explanation for the flatness might be that we live in flat Minkowski space. However, we still have to tune the explosion to be such that it does not collapse back into a black hole quickly. Maybe there is a law of nature which says that the explosion has to disperse indefinitely and it cannot collapse back?

The Milne model

We have suggested in this blog that the total gravity charge of the observable universe is zero. Then the expansion would continue at a constant speed with no deceleration.

https://en.wikipedia.org/wiki/Milne_model

Does this solve the flatness problem?

https://en.wikipedia.org/wiki/Flatness_problem

Currently, the mass density of the observable universe seems to be about 30% of the critical density ρc of the standard Big Bang model.

In the Milne model, the Hubble "constant" is

       H = C / t,

where C is a constant and t is the time from the explosion.

How does the density of mass-energy ρ develop in the Milne model?

If a is the scale factor, the apparent energy density of photons declines as

       ~  1 / a⁴,

because the observer sees arriving photons redshifted.

The energy density of massive particles declines roughly as

       ~  1 / a³.

The problem becomes:

Why is the density ρ of the same order of magnitude as ρc now that 13.7 billion years has passed since the explosion? The value of ρ could be much larger or much less. It was much larger at a time t = 10 million years, and it will be much less at a time t = 1,000 billion years.

In the Milne model the spatial metric is always flat because the total gravity charge is zero. The fine-tuning is in the mass-energy density of ordinary and dark matter, relative to the critical density ρc.

Let us change the mass-energy density ρ somewhat, say, 50% from the current value. Let us then calculate backward the history of the universe. In the Milne model, the universe would have roughly the same history as we know it, but the mass-energy density would be 50% larger at every stage. The Milne model does not require a fine-tuning of the density to one part in 10⁶⁰ in the early stages, like the FLRW model does.

What evidence is there that the topology of the observable universe is as in the FLRW model?

The angular spectrum of temperature differences in the cosmic microwave background is rather "uniform", with some bumps and troughs. Supporters of the inflation hypothesis believe that inflation would create such a spectrum from "random quantum fluctuations" in a tiny primordial space.

Such random fluctuations could occur also in a newtonian explosion.

The troughs and bumps in the spectrum are explained by "baryonic oscillation" of matter soon after the Big Bang. We admit that this does support the FLRW model, though the same process might happen also in a newtonian explosion.

Conclusions

If we are able to show that a "metric" cannot describe the gravity field, then it is very unlikely that a curved spacetime like that in the FLRW model would exist. Far more probable is that the metric of spacetime is Minkowski, and the Big Bang is an ordinary, newtonian explosion. The Big Bang is not the start of the entire universe.

The Big Bang is very much like a newtonian explosion also in the FLRW model. Occam's razor implies that we should not assume the FLRW model at all, but stick to the simplest explanation: an ordinary newtonian explosion.

The Milne model removes the need for an extreme fine-tuning of the mass-energy density ρ in the early stages of the universe. Our observation is a serious blow to the Big Bang plus inflation hypothesis. The volatility of the Big Bang model is a result of the Einstein equations. The inflation hypothesis is highly speculative. We may interpret the history of modern cosmology since 1922 in this way:

1.   People tried to apply to cosmology erroneous Einstein assumptions about curved spacetime.

2.   They obtained the FLRW model which is extremely volatile for initial conditions. This was a sign that the model is wrong.

3.   Alan Guth and others in the 1980s tried to fix the volatility problem with a very speculative inflation hypothesis.

4.   It was found out that also the inflation hypothesis has to be fine-tuned to make inflation to work! Paul Steinhardt has criticized the inflation hypothesis on these grounds.

5.   The expansion is not slowing down as expected. People invented a speculative cosmological constant, or dark energy, to explain this. The Milne model probably does not need dark energy to explain the astronomical observations.

This history of cosmology reminds us of the tower of turtles cosmological model:

https://en.wikipedia.org/wiki/World_Turtle

https://en.wikipedia.org/wiki/Turtles_all_the_way_down

Gravitating mass, inertia, and centripetal acceleration

In general relativity, the gravity potential steepens at low radii r, relative to the newtonian potential.

                       ●  M

                       r

                   m •     

                       |   

                       |   rope

                       | 

                       |   ^

                       |   |  F force

                       |

                         \ o

                            |

                           /\    observer

An observer uses a rope to lower a test mass m very slowly close to a mass M. Let us calculate the potential very naively.

The remaining fraction of the mass-energy of a static test mass is

       sqrt( 1  -   (2 G M / c²) / r ).

The remaining mass-energy is zero at the Schwarzschild radius

       rₛ  =  2 G M / c².

In the newtonian potential, the remaining fraction of mass-energy is

       sqrt( 1  -  (G M / c²) / r ).

It is zero at

       rₛ / 2  =  G M / c².

The horizon radius in the newtonian potential is just 1/2 of the Schwarzschild radius rₛ.

What is the gravitating mass of m?

In the above equations we assumed that the gravitating mass-energy of a test mass m remains m when it is lowered close to M. That is a reasonable assumption if m falls freely toward M and the potential energy which m loses is converted to kinetic energy of m.

But we used a rope to lower the mass m slowly. It did not gain kinetic energy.

The paradox is solved by the fact that the field of M shortens the rope as we lower m downward. The observer can let the force F do work for a surprisingly long additional length of the rope.

The gravitating mass of m and the force F do shrink according to the fraction

       sqrt(...),

but that is compensated by the radial metric stretching according to

       1 / sqrt(...).

The gravity force F shrinks to zero when m is at the horizon.

A perpetuum mobile? No

Let us lower the test mass m in such a way that first it is allowed to gain kinetic energy. After a while, we let it fall at a constant radial coordinate velocity.

The gravitating mass of m is larger than with the slow lowering procedure. Gravity does more work for the whole trip down. Can we recover more energy this way?

No. If we let m fall freely to some distance r from M, its total mass-energy, measured from far away, is still m c². Lowering that mass-energy from the distance r to the horizon will give the energy m c² to the observer – no more.

Energy is conserved. In this context, the notion of "work done by gravity" is misleading.

If we lower the mass m slowly with a rope, we extract the energy from m at larger radii than in the partial free fall case. That is the difference between the two procedures.

The centripetal force and acceleration

To keep a test mass m on an orbit, gravity must give it enough acceleration. The inertia of the test mass m tries to make the test mass to fly along a straight line.

                          ● M

                                       ^ 

                                     /

                      •  ---------

                     m

Thus, the centripetal force is gravity. Crucial in this is what is the inertia of m in this configuration.

We have claimed in this blog that the inertia against a tangential acceleration relative to M is

       m / sqrt(1  -  rₛ / r)

and the inertia against a radial acceleration is

       m / (1  -  rₛ / r).

Which is the relevant inertia on a circular orbit?

Let us look at circular orbits in the Schwarzschild metric.

https://en.wikipedia.org/wiki/Schwarzschild_geodesics

There μ = m, because we assume that m is very small. The angular velocity ω in the Schwarzschild metric is the same as in newtonian gravity. Is this a coincidence?

If we believe the Schwarzschild metric, then the gravitating mass of m is its total mass-energy, and its inertia on a circular orbit has to be the same, because m stays on the newtonian orbit.

This is strange. The gravitating mass-energy of a static m is

       m sqrt(1  -  rₛ / r).

Can its inertia against the acceleration on a circular orbit be that low?

The acceleration on a circular orbit is neither tangential nor radial. The tangential and the radial velocities stay constant. Thus, the inertia might be that low.

The extra inertia in a tangential motion of m relative to M would be a separate "load" that m has to carry, but that load would "naturally" orbit M so that m does not need to exercise a force to keep the load on a circular orbit. The following mechanical model would explain this:

              <-- ω

              _____      ring of inertia

            /            \

           |      ● M  |  

            \______/

                   • --> v

                  m

When m comes close to M, m attaches itself to a "ring of inertia", which slows down the tangential motion of m. Once m is attached to the ring, the extra inertia does not affect a circular orbit of m. The ring rotates around M at an angular velocity ω without any extra effort.

The extra inertia is a property of the common field of m and M. The inertia is not an independent body which could fly around on its own. It is not strange at all that the extra inertia can stay on a circular orbit without any extra effort from m.

Similarly, the extra inertia does not increase the gravitating mass of m.

The circular orbit of a photon around M

Let us calculate the coordinate radius for a circular orbit of a photon around M.

The tangential velocity of a photon is

       v = c  sqrt(1  -  2 G M / c² * 1 / r).

We have

       G M / r²  =  v² / r

   <=>

       G M  =  v² r

                =  c² r  -  2 G M

   <=>

       r  =  3 G M / c²

  

           =  3/2 rₛ.

If we use a newtonian gravity potential, then

       v  =  c  (1  -  G M / c² * 1 / r),

       G M  =  v² r

                 =  c² r  -  2 G M  +  G² M² / c²  *  1 / r

   <=>

       0  =  c² r²  -  3 G M r  + G² M² / c²

   <=>

       r  =  3/2 G M / c² 

         +- sqrt(9 G² M²  -  4 c² G² M² / c²)  /  (2 c²)

           =  3/2 G M / c²

               +- sqrt(5) / 2 * G M / c².

The sensible value is

      r  =  (3/2 + sqrt(5) / 2)  G M / c²

          =  2.62 G M / c².

Conclusions

The gravitating mass of m close to a mass M is

       m  sqrt(1  -  rₛ / r),

where rₛ = 2 G M / c². The inertia of the gravitating mass alone is the same

       m  sqrt(1  -  rₛ / r).

Also, m feels extra inertia if its tangential velocity or its radial velocity changes. The total inertia of m for a tangential movement is

       m / sqrt(1  -  rₛ / r)

and for a radial movement

       m / (1  -  rₛ / r).

It is not a coincidence that circular orbits in the Schwarzschild metric obey the newtonian equation. The gravity force is newtonian, and the gravitating mass of m is the same as its inertial mass, for a circular motion.

Flaws in general relativity: a summary

UPDATE November 13, 2023: The question of Lorentz covariance of general relativity is still unclear. On November 7, 2023 we tentatively proved that the Einstein equations have no solution for any realistic physical system. The question of Lorentz covariance becomes partially moot.

We are undecided about linearity/nonlinearity of gravity.

----

Let us summarize our findings so far about what is wrong and right in general relativity.

What is wrong in general relativity

1.  The Einstein field equations are not Lorentz covariant. They calculate a wrong orbit for a test mass m in the case where the central mass M moves. The reason is that the field equations think that the kinetic energy of M gravitates like the rest mass of M, while the gravitational pull really is fourfold, if m passes past M.

2.  The steepening of the gravity potential in the Schwarzschild solution is highly suspect: it leads to very strange results. The potential probably has to be newtonian.

3.  General relativity does not satisfy a weak equivalence principle. Though this is not really wrong, since we do not think that gravity should satisfy it.

4.  The concept of a "metric" handles accelerating gravity sources in a wrong way. We may be forced to abandon the concept of a metric and treat the interactions between the test mass m and the parts of M "privately".

5.  If gravitational waves truly can shorten spatial distances between two events, they open a way for superluminal communication. That has to be prevented.

6.  The Gödel universe and the Kerr solution seem to contain timelike loops. That is unlikely to be a physically correct prediction.

7.  The claim that spacetime can be "curved" and that its topology can differ from the Minkowski space is a bold hypothesis, for which we have no evidence whatsoever. The hypothesis is almost certainly wrong.

What is correct in general relativity

1.  In the weak field, the Schwarzschild solution seems to be right. It agrees with our own Minkowski & newtonian gravity model.

2.  The geodesic equation calculates orbits correctly for a metric (if there exists a correct metric).

3.  Linearized Einstein equations calculate the energy content of gravitational waves correctly.

All "exotic" black hole physics is incorrect

1.  It is very unlikely that a one-way membrane  like the event horizon, can exist physically. The system probably "freezes" before such a strange object can form.

2.  A singularity does not make much sense. The freezing process probably prevents a singularity from forming.

3.  Black hole thermodynamics is entirely wrong. There is no need for a black hole to have large entropy.

4.  Hawking radiation does not exist. There is no black hole information paradox.

Conclusions

General relativity got right weak field gravity effects, like the bending of a ray of light as it passes the Sun, and gravitational waves. There has to be some truth to the Einstein field equations, even though they handle moving masses incorrectly. We have to analyze what exactly is right in the field equations. Equivalence principles might be the reason why the field equations get some things right.

In July 2023 our goal was to find out if we can disassemble a black hole by spinning it fast. We now know more about gravity, and can try to resolve the question.

Private interactions and the metric give contradictory results

In our previous blog post we claimed that "private interactions" between the test mass m and the parts of a mass flow can give a different acceleration for m than what we get if we sum the metric perturbations for each part and use the metric to determine the acceleration.

This is a surprising result because one would guess that the acceleration is linear in perturbations.

The metric of a mass flow

Let us determine the metric of the mass flow which we introduced in the previous blog post.

            1                                 3

                \                           /          ^

                  \                       /          /   v

                    \__________/

                             2

                             ^   V

                             |

                             •  m

We sum the metric perturbations for each part of the mass flow. We are interested in the metric close to the test mass m. The parts 1 and 3 point directly at m.

https://en.wikipedia.org/wiki/Lorentz_transformation

Let us first determine the metric perturbation which is caused by the part 1 of the mass flow.

                               

                      r' = distance (M', m)

                  M'

          -------•-----------                        • m

         R₂                   R₁     

         ρ = mass / length

              mass flow

     ------> x

Let us temporarily choose the part 1 as the x axis. Then it is easy to calculate the perturbation at m, which is also located on the x axis. Let the moving frame be comoving with the part 1. Let us have ρ dr as a mass element of the flow 1.

Then the line element for the metric around ρ dr is:

       ds²  =  (-1  +  rₛ / r')  dt'²

                + (1  +  rₛ / r')  dr'²

                + (r' dφ')².

We write

       dr' =  dx',

       r' dφ' = dy',

because the contribution to dr' from dy' close to m is essentially zero. Then

       ds²  =  (-1  +  rₛ / r')  dt'²

                + (1  +  rₛ / r')  dx'²

                + dy'².

The Lorentz transformation gives:

       dt'   =  γ dt  -  γ v / c²  *  dx,

       dx'  =  γ dx  -  γ v * dt,

       dy'  =  dy.

Let us set c = 1 to simplify the calculations. The metric in the laboratory frame is

       ds² =  γ²  (-1  +  rₛ / (γ r))

    

                         * (dt²  -  2 v dt dx  +  v² dx²)

                + γ²  (1  +  rₛ / (γ r))

                         * (dx²  -  2 v dt dx  +  v² dt²)

               + dy²

              =  γ²  (-1  +  rₛ / (γ r)  +  v²)  dt²

                 + γ²  (1  +  rₛ / (γ r)  -  v²)  dx²

                  - 2 γ v  rₛ / r  *  dt dx

   

                  - 2 γ v  rₛ / r  *  dx dt

                 + dy².

Note that the metric is at one moment of the laboratory coordinate time t. Since the part ρ dr is moving at a velocity v, the metric is time-dependent.

We dropped the terms ~ v² rₛ, because we assume that rₛ  <<  v  <<  1. The metric is almost orthogonal since v rₛ is very small.

To obtain the metric near m, we need to integrate over the radii R₁ + x to R₂ + x, where x is the displacement from the test mass m on the x axis. That is, we set x = 0 at m.

However, in the geodesic equation we are interested in the derivatives of the metric g. It is better to calculate the derivatives directly.

The perturbations of individual parts ρ dr are time-dependent. But the sum of all the perturbations is time-independent. The time derivatives of the integrated metric are zero. It is enough to calculate the derivatives with respect to x and y.

We have:

       dgₜₜ / dx  =  dgₓₓ / dx

                                       R₂ + x

                          =  2 γ      ∫      G ρ / r²  *  dr

                                     R₁ + x

                          =  2 γ G ρ

                              *  (1 / (R₂ + x)  -  1 / (R₁ + x))

                          = 2 A(x),

where A(x) is the newtonian gravity acceleration caused by the mass in the part 1.

We have

       dgₜₓ / dx   =  dgₓₜ / dx

                            =  -4 v A(x).

The acceleration from the geodesic equation

https://en.wikipedia.org/wiki/Geodesics_in_general_relativity

          1

              \  

                \      \      v

                  \      v   

                           β

                          \   ^    V

                            \ |

                              •  m

                                \

           y                     v   a

     __--->               

     \  

       \   

        v  x

Using the coordinates of the previous section, the velocity of m is

       Vₓ  =  -V cos(β),

       Vy  =   V sin(β).

We are interested in the acceleration of m to the x and y directions. The y acceleration relative to the proper time τ of the test mass m is

       d²y / dτ²  =  0,

that is, the y velocity Vy slows down as the proper time of m slows down. The Christoffel symbols relevant for the x acceleration are:

       Γₓₓₓ  =   A(x),

       Γₓₜₜ    =  -A(x),

       Γₓₜₓ   =  4 v A(x) - 4 v A(x)  =  0,

       Γₓₜₜ   =  4 v A(x) - 4 v A(x)  =  0.

The acceleration is

       d²x / dτ²  =  1 / gₓₓ(x)

                          * ( A(x) * (dx / dτ)²

                              + A(x) * (dt / dτ)² )

   <=>

       d²x / dt²  =  1 / gₓₓ(x)

                          * ( -A(x) V_x² + A(x) ).

The accelerations do not depend on the sign of v. If we calculate the accelerations due to the part 3 of the mass flow, they are symmetric relative to the the part 1. This means that the parts 1 and 3 do not cause any horizontal acceleration.

The part 2 does cause acceleration to the right.

If we calculate the accelerations using the private interaction model, the result agrees for the part 2, but does not agree for the parts 1 and 3. In the private model those parts cause acceleration to the right.

The accelerations of the mass flow in the turns of the flow between 1 and 2, and 2 and 3, contribute a net acceleration straight up.

Thus, the private interaction model gives a different result from the metric.

How can a metric perturbation be "nonlinear" in such a way that the sum gives a different acceleration from the sum of individual accelerations?

       1

           \

             \

               \________   2

                    ---> v    

                       ^   V

                       |

                       • m

The reason is that the metric does not understand what happens when a mass element ρ dr turns from the part 1 to the part 2. Thus it is the acceleration of the mass elements, after all, which spoils the calculation with the summed metric perturbation.

The acceleration of m is due to it diving deeper into the gravity field of the moving mass elements ρ dr in the part 1 of the mass flow. But when an element comes to the turn between 1 and 2, the element suddenly "disappears" from the integral. The potential of that element vanishes and m magically jumps up into a higher potential.

Can we somehow fix the metric so that it would not be confused by this case?

The "private interaction" model does handle this.

The metric should be augmented with a mechanism which tells us what happens to the test mass m when a mass element is accelerated.

A partial solution: calculate the metric letting the parts of M "fly loose"?

Since the metric cannot handle an acceleration of a mass element of M, let us remove all the accelerations for a short moment. All the parts of M fly freely and there is no acceleration in their path. Then we can calculate the sum of the metric perturbations.

Though this will not work if the acceleration of the mass elements happens to impose an "important" acceleration just at that moment.

Also, the solution only works for a short moment, as the free-flying parts of M soon are dispersed and do not describe the true state of M any more.

In the case of a rotating disk, letting the parts "fly loose" makes the configuration and the metric time-dependent. It is not a beautiful solution.

Conclusions

We were able to solve the mystery of why the calculations on August 10 and August 29, 2023 gave different values for the frame dragging by a rotating disk. Our August 10 calculation claimed that the gravitomagnetic moment is 1/2 J, while the August 29 calculation said that there is no frame dragging at all. The reason is that the concept of a "metric" does not understand a configuration where parts of the mass M are under an acceleration.

The value for the gravitomagnetic moment of a rotating disk is 2 J in the literature. We believe that value is incorrect.

It is not clear if we can mend the concept of a metric to handle mass elements which are under an acceleration. If not, then the "private interaction" model, which we have introduced, is the correct way to describe a many body system where the parts are accelerating.

Gravity of an accelerating mass M

Now that we have gained a lot of experience about inertia, metrics, and the geodesic equation in the past two months, it is time to revisit the mystery (solved?) on September 3, 2023. Can we get conflicting results for two methods:

1. we calculate the Schwarzschild acceleration of m for each part of M, and sum the accelerations;

2. we sum the metric perturbations for each part of M and then calculate the acceleration of m using the summed metric?

If M, for example, is a rotating disk, its parts are under a constant centripetal acceleration. We suspected on September 3, 2023 that the acceleration of the parts spoils the method 2 above.

We did get consistent result for a moving cylinder on August 28, 2023, using the methods 1 and 2 above. The cylinder moved at a constant speed, no part of it was under an acceleration.

An accelerating M and a test mass m by its side

                       M

                        ● -----> a_x

                        r

                        • --> a_x'

     ^  y            m

     |

      -------> x

Both M and m are initially static. The mass M starts to accelerate right. What happens to m?

Our own Minkowski & newtonian gravity model suggests that M pulls m along with it. The masses M and m share some inertia. The inertia starts to accelerate with M.

The mass m has gained the extra inertia

       m  *  1/2 r_s / r

in the field of M. This extra inertia resists movements of m in the field of M. If M starts to accelerate, then we can guess that the inertia tries to keep m moving along with M.

If m is very close to the horizon of M, then the speed of light there relative to M can be tiny, as observed by a faraway observer. The test mass m must move along with M  –  otherwise it would break the speed limit.

Does the metric of general relativity say anything about the problem?

Let us imagine that M has already gained a tiny velocity v, and m is somehow "thrown" into the metric of M. The test mass m "enters" the field of M at the opposite velocity -v.

If m enters the field of M from far away, the slow metric of time close to M slows down the movement of m, as shown by the constants of motion for the Schwarzschild metric: if the proper time of m slows down, so does its velocity.

We can guess that m attains an acceleration

       a_x'  =  a_x  *  (1  -  1 / sqrt(1 + r_s / r))

in the diagram above. If r is large, then the value is

       a_x'  =  a_x  *  1/2 r_s / r.

The test mass m behind M

               m

                • -->              r             ● -----> a_x

                a_x'                          M

       -----> x

In the radial direction, m has double the extra inertia of the tangential direction. Both m and M are initially static. Then M starts to accelerate to the right. What is the acceleration a_x' of m?

The formula might be

       a_x'  =   a_x  * 2 (1  -  1 / sqrt(1 + r_s / r))

                =   a_x  *  r_s / r,

for large r.

Can general relativity suggest the same formula? Yes. If we "throw" m to the metric of M, m loses coordinate velocity because its proper time τ slows down, and because the radial metric is stretched. We obtain a double effect relative to the "by the side" case.

Does this affect the field of a rotating disk?

                     <--  ω

                       ____

                    /          \

                    \_____/

                        ^   V

                        | 

                        • m

Every part of the disk accelerates toward the center of the disk. The parts close to m share more inertia with m. There might be an additional force which pulls m toward the disk if m is static? We are not sure.

Suppose then that m approaches the disk at a velocity V. Then m starts to share more inertia with the near part of the disk than with the far part. This is the traditional magnetic force which we have always included in our calculations.

Could there be a subtler mechanism through which the acceleration of the parts of the disk pulls m to the side?

We wrote on September 3, 2023:

"If we let the disk parts fly loose, so that there is no acceleration in their paths, then the parts on the left of the disk really start a collective movement toward the test mass, and our argument on August 10 that the left parts are "approaching" the test mass faster, is true.

But in a rotating disk, the collective field of the left side of the disk is time-independent. The collective field is not approaching the test mass faster on the left than on the right."

The discrepancy between the August 10, 2023 calculation of the sum of the accelerations, and the August 29, 2023 sum of the metric perturbations probably came from the fact that the acceleration calculation lets the parts of the disk "fly loose", without being accelerated toward the center of the disk. The situation is "dynamic".

The sum of the metrics, on the other hand, takes into account that the parts cannot fly away, they are stuck to their position in the disk. The metric becomes time-independent.

Which is the correct way to calculate? Probably neither one. They both ignore the acceleration of m when its extra inertia bound to a part of disk accelerates as the disk turns.

The magnetic effect of a simple mass flow

Let us analyze a simpler configuration:

                  1                            3

                      \                      /          ^

                        \                  /          /   v

                          \_______/      mass flow

                                2

                                ^  V        ^

                                |              |  F' force

                                 •  m

                                   \

                                     v    F force

                                  \   F''

                                   v 

                                      ^

                                        \  F'''

    ^ y

    |

     -------> x

We tune V and v so that the mass in the part 3 of the mass flow is almost static relative to the test mass m. The parts 1 and 3 point directly toward m.

When m moves toward the mass flow, it acquires inertia from the mass flowing at the part 1 of the mass flow. The acquired inertia pushes m down to the right with a force F.

The acquired inertia is "carried" by the mass flow from the part 1 to the part 3. The inertia accelerates upward when it takes the turns as it moves from 1 to 3. This exerts another force F' which pushes m up.

The force F' partially cancels the y component of F. The net force

       F + F'

pushes m to the right, and also down.

We conclude that the parts 1 and 2 do exert a "magnetic", horizontal force on m. If we let the parts 1 and 2 "fly loose", so that they do not turn at the bends of the mass flow above, then the effect is essentially the same as for the configuration where the mass flow takes the turns (= accelerates at the turns).

Let us then analyze the extra inertia which m acquires as it approaches the horizontal part 3. The extra inertia pushes m to the right and down with a force F'' but when the extra inertia turns to the part 3, it accelerates to the left and and pushes m up and to the left with a force F'''. Note that if we naively calculate the metric of the mass flow, it is not aware of the force F'''.

The sum

        F + F' + F'' + F'''

pushes m down and to the right.

Since the part 1 is length contracted, gravity pulls m more to the left. Does this cancel the entire magnetic effect of the mass flow? Probably not. If V is much larger than v, then we can ignore all effects ~ v².

Let us analyze under the assumption V >> v.

1.  F_x ~ v V,

2.  F_x' ~ v V,

3.  F_x'' ~  v V,

4.  F_x'''  ~  v V.

All the forces are relevant.

We have yet another force F'''' which is caused by the part 3 slowing down m as m approaches 3.

The force which the part 1 exerts on the test mass m is, to a larige extent, due to the slowing down of the time close to 1. If we imagine that the part 1 "flies loose", then m approaches the slow time zone of 1 at a velocity ~ V + v, while it only approaches the slow time zone of 3 at a velocity ~ V - v. The configuration is asymmetric horizontally.

However, the metric close to 1, 2, 3 is time-independent, and the time runs at about the same rate close to 1 and 3. The metric does not reveal the time asymmetry between 1 and 3.

Accelerations probably are not too relevant, after all

       

                  <--- ω

                   ____

                /          \       M

                \_____ /      

           

                     •  m

      ^ y

      |

       ------> x

Consider again the case of a rotating disk. The configuration is almost symmetric in the x direction. On the left side the parts are accelerating to the right. Some inertia of m accelerates right, causing a force F on m to the positive x direction.

But the force F is canceled by the corresponding effect on the right side.

The acceleration of the far side pushes m down and the acceleration of the near side pulls m up. The sum of forces pulls m upward, but there is no horizontal force.

Conclusions

We now have a very simple hypothetical formula which tells us how the acceleration of M affects a test mass m.

The discrepancy in our calculations of the magnetic effect of a rotating disk on August 10 and August 29, 2023 is not explained by the centripetal acceleration of the parts of the disk.

The discrepancy, probably, is due to the fact that the acceleration of m has to be calculated from its "private" interaction with each part of the disk. If we first sum the metric perturbations for each part, we lose information which is required in calculating the acceleration. This means that the concept of a "metric" is flawed, as we have suspected for the past two months. We will write a new blog post which examines in detail this question.

The gravity of a mass M moving back and forth

Let us return to this crucial question once again. We assume that M / r is small.

The effect of the stretched radial metric around M, in the comoving frame of M

                                M

                                 ●

                                 r

                     v  <---- • m

                          p_t'

      ^ y'

      |

       ------> x'

We work in the Schwarzschild coordinates in the comoving frame of M. We learned today that the geodesic equation is aware of the (spurious) coordinate acceleration caused by the stretched radial metric around M. Let v << c.

When m moves to the left, some of its tangential momentum p_t' is converted into radial momentum p_r'. But the spatial metric is stretched in the radial direction. Coordinatewise, the test mass moves surprisingly slowly in the radial direction, though its momentum is as expected.

                                                      ●  M

             ^      v_t'                r

                  \

                       \

                          •  m

                       /

                     /

                  v      v_r'

The radial velocity vector v_r' is surprisingly short after a while. The test mass appears to move up to the positive y direction. There is a coordinate acceleration up, caused by the stretched spatial metric.

Let us calculate this effect. Let m be right below M at the time 0. At a time t', m has moved a distance

        x'  =  v t'

from directly below M. The radial velocity then is

       v x' / r.

The radial velocity, coordinatewise, is surprisingly slow by the amount

       1/2 r_s / r  *  v x' / r

       =  1/2  *  2 G M / c²   *  v² t' / r²

       =  t' * G M v² / c²  *  1 / r².

We have as the apparent acceleration to the y direction:

       a_y'  =  γ² G M / r².

It is as if M would have the gravity of

      M v² / c²

of additional mass, that is, twice the kinetic energy of M, if M would move at the speed v.

Calculation using the geodesic equation in the Schwarzschild metric

https://en.wikipedia.org/wiki/Geodesics_in_general_relativity

             |                  |  y 

             |                  |

                    v

                 <--- • m

              ------------------ 

                       x

Let us have the Schwarzschild metric around M. We take a small patch around m, and construct a y coordinate and an x coordinate in a way that the coordinates are orthogonal and their metric at m is

        1         0

       

        0         1

The coordinates of m are

       (x, y) = (0, 0).

It is not exactly a flat metric because the r metric is stretched, or equivalently, the circumference of M at a radius r - y is "too long". If we would shrink the circumference of M at a radius r - y by a factor

       1  -  y / r * 1/2 r_s / r,

then it would be a flat metric. We conclude that in our x, y coordinates, the x metric g_xx at y is

       g_xx(y)  =  1  +  y / r  *  r_s / r.

Since dy / dt = 0, in the geodesic equation, only the first term matters. There, μ = y, and α and β can be t or x, because dt / dt and dx / dt are non-zero.

Let us calculate the acceleration which is due to the changing spatial metric of x when we vary y:

       Γ_yxx  =  -1/2 dg_xx / dy

                   =   -1/2 * r_s / r².

Raising the y index has a negligible effect is M is not heavy. We obtain:

       a_y''  =  1/2 * 2 G M / c² * 1 / r² * v²

                 =  G M v² / c²  * 1 / r².

It is the gravity of twice the kinetic energy of M, if the speed of M were v.

The geodesic equation agrees with our result in the previous section.

Switch back to the laboratory frame

                          M 

                           ● ----> v

                              r

                          ^  a_y

                          |

                          • m

      ^  y

      |

       ----->  x

The test mass m is initially static. The Lorentz transformation of accelerations tells us that

       a_y'  =  a_y  /  γ².

We get a surprising result:

        a_y  =  γ⁴ G M / r².

The extra gravity is as if the kinetic energy of M would gravitate fourfold. How can we explain such a large gravity?

We probably do not need to explain it. The natural frame to study the gravity is the comoving frame of M. If we switch to the comoving frame of m (= the laboratory frame), there a clock ticks slower by a factor 1 / γ, and the observer, cobsequently, measures the acceleration to be γ²-fold.

If the test mass m moves back and forth

                             ● M

                              r

                                m

                  -v <---- • ---> v

                              |

                              |   rope

                              |

                                 |    pull

                                 v

       ^  y

       |

        ------> x

We work in the Schwarzschild coordinates. The test mass m starts from directly under M, at coordinates

    (t, x, y)  =  (0, 0, 0).

Let m initially possess a momentum

       p(0) = γ m v,

which is purely to the positive x direction. Clocks tick slower close to M, which causes a "temporal" acceleration

       a'  =  G M / r²

toward M. The associated force is

       F'  =  γ m a',

and the cumulated momentum

       p'(t)  =  t F',

which is almost exactly to the positive y direction. We divide the current momentum of m into parts:

       p(t)  =  p'(t)  +  p''(t).

Let us imagine that we remove the momentum p'(t) by pulling m away from M with a rope. The remaining part of the momentum is

       p''(t).

Its behavior depends on the spatial metric around M. Our goal is to prove that p''(t) varies cyclically with time, and there is no cumulation of p''(t) with time.

In our own Minkowski & newtonian gravity model, the apparent stretching of the radial metric is caused by the inertia of the field energy E which flows to m if m approaches M, and away from m if m recedes from M. The energy flows over a distance r.

                        ● M

                          

                            ^  E energy flow

                              \    

                                \  r

                                  \ 

                                    \

                                      •  ---> v

                                     m

In the diagram, m is receding and its kinetic energy flows to back to the common field of M and m, over an average distance r.

The energy flow causes extra inertia to m in a radial motion. The inertia tries to resist m from moving farther from M.

If m moves back, the inertia resists m coming closer to M.

The process looks cyclic, with no net change in p''(t) over a cycle. We may imagine a system of levers which forces m to transport some weights over the distance r if it wants to move farther from M. If m wants to move closer, it has to move the weights back. If we apply a horizontal alternating force to m, the effects cancel each other and there is no cumulation of p''(t).

We conclude that only the temporal acceleration a'  =  G M / r² affects the y velocity of m in the long run.

The force caused by the temporal acceleration is

       F' =  G γ m M / r².

The gravity charge of m is γ m.

What if m is static and M moves back and forth?

We already calculated what happens if m moves back and forth. The gravity force is, on the average,

       G γ m M / r².

The same should hold for M. Its gravity charge becomes γ M.

Conclusions

We hope that we finally got right the acceleration of m caused by a mass M moving monotonically to a certain direction.  The acceleration has to be calculated in the comoving frame of M, using the Schwarzschild metric. The acceleration is surprisingly large, as if γ⁴ M were the gravity charge in the case where M moves tangentially relative to m.

If M moves tangentially back and forth, then the gravity charge is, on the average, γ M, as we would expect. We have to calculate the accelerations for a non-tangential motion of M later.

Our model is Lorentz covariant because the accelerations are calculated in the comoving frame of M and then Lorentz transformed to the desired frame.

We wrote on September 16, 2023 that there probably is no steepening of the gravity potential relative to the newtonian potential. The Schwarzschild metric should then be replaced with a "newtonian metric":

     -1  +  G / c² * M / r    0                              0

     0                     1 + G / c² * M / r                0

     0                                       1 + G / c² * M / r

Correct Lorentz transformation for the electric field E_x

UPDATE October 6, 2023: We corrected the error in our Lorentz transformation of E_x. The electric field in a frame has to be measured with a test charge q which is static in that frame.

Our error was to assume that the "inertia" of the test charge is the same as its mass-energy γ m.

----

We wrote on September 9, 2023 that the Lorentz transformation of the electric field, E_x' = E_x is incorrect in the Feynman Lectures on Physics (1964), as well as in all the other literature. We were wrong.

https://en.wikipedia.org/wiki/Classical_electromagnetism_and_special_relativity

https://www.feynmanlectures.caltech.edu/II_26.html

The Feynman Lectures on Physics (1964) contains the same formulae as Wikipedia.

A lemma: the acceleration of a moving mass m under a force F

Let us have a moving mass m with a velocity v and a force F which accelerates it to the direction of v. What is the acceleration of m?

                       --->  F

                     • ---> v

                    m

The total energy of m is

       W  =  m c² / sqrt(1  -  v² / c²).

When m moves a time dt, it gains the energy

       dW  =  F v dt.

We have

       dW / dv  =  m c² * -1/2 * (1  -  v² / c²)^-3/2

                          * -2 v / c²

                       =  m v γ³.

Then

       dv  =  dW / (m v γ³)

              =  1 / γ³  *   F / m  *  dt

The acceleration is like the newtonian one, but must be corrected by the factor 1 / γ³.

The correct transformation is E_x' = E_x

                   a_x                         

                  • --->                      ● 

                 q                             Q

                 m

     ^ y

     |

      ------> x

                      ^ y'

                      |

                       ------> x'

                        ---> v

Let us have the following configuration in the laboratory frame. The test charge q is initially static and its mass is m. The charge Q is static.

Let us switch to a frame which moves to the positive x direction at a speed v. We denote

       γ  =  1 / sqrt(1  -  v² / c²).

We denote parameters in the moving frame with the prime '.

https://en.wikipedia.org/wiki/Acceleration_(special_relativity)

We have

       a_x  =  q E_x / m.

The test charge q does not feel a magnetic field in the laboratory frame or the moving frame, only an electric field.

The Lorentz transformation of the acceleration is:

       a_x'  =  a_x / γ³.

Our test charge q is not static in the moving frame, but has a velocity v to the negative x' direction.

                --> A_x

              • --> v                   ●

             q'                           Q

             m

Let us use a test charge q' which is static in the moving frame. Its acceleration in the laboratory frame is

       A_x  =  a_x / γ³.

Let A_x' be the acceleration of q' in the moving frame. In that frame, q' is static. Then

       A_x  =  A_x' / γ³.

We obtain

       A_x'  =  a_x.

That is, the electric field measured in the moving frame is

       E_x'  =  E_x.

The transformation E_y' = γ E_y is approximately correct if Q and q are static

                         ●   Q

                          

          

                         • q 

                           m

    ^  y

    |

     -----> x

Let us switch to a moving frame, the speed is v to the positive x direction. We have:

       a_y' =  q / (γ m)  *  (v × B_z'  +  E_y'),

       a_y  =  q / m  *  E_y,

and

       a_y'  =  a_y / γ².

Let us assume that v is slow. Then

       B_z'  =  -v C / c² * E_y 

where C is very close to 1.

We have

       q / (γ m)  *  (-v² C / c²  *  E_y + E_y')

       =  q / m * 1 / γ² * E_y

<=>

       E_y'  =  1 / γ  *  (1  +  γ C  v² / c²) E_y.

There γ C is close to 1, and approximately,

       E_y'  =  1 / γ * (1 + v² / c²) E_y

                =  γ E_y.

A moving Q and a static q

                     Q

                     ● ---> v

                     • q

                       m

     ^  y

     |

      -----> x

In the laboratory frame, approximately,

       B_z  =  v / c²  *  E_y,

       a_y  =  q / m  *  E_y.

In the comoving frame of Q,

       a_y'  =  q / (γ m)  *  E_y',

and

       a_y'  =  a_y / γ².

Then

       E_y'  =  E_y / γ.

Let us check the what Wikipedia says that E_y' should be:

       E_y'  =  γ (E_y  -  v B_z)

                =  γ (E_y  -  v² / c² E_y)

                =  E_y  γ * 1 / γ²

                =  E_y / γ.

Transformation of the magnetic field B_z if Q and q comove

                     Q

               v <--- ●

                      .  .  .  B_z'

               v <--- •

                        q

                        m

        ^ y

        |

         -----> x

In the diagram we have a moving frame. In the laboratory frame Q and q are static.

Let us assume that Q is positive and q negative. The magnetic field B' lines point out of the screen (marked with . ). The magnetic force on the test charge,

       F_y'  =  q v × B_z'

points down in the diagram. The acceleration is

       a_y'  =  q / (γ m)  *  (v × B_z'  +  E_y').

Let us switch to the laboratory frame. There

       a_y / γ²  =  a_y'

                      =  q / m  * 1 / γ * (v × B_z' + E_y')

                      =  q / m  *  γ E_y'

   <=>

       (γ² - 1) E_y'  =  v × B_z'

   <=>

       B_z'  =  -(γ² - 1) / v * γ E_y.

Approximately,

       -(γ² - 1) / v  =  -v² / c² * 1 / v

                            =  -v / c².

The Lorentz transformation in Wikipedia is approximately correct in this particular case. Wikipedia claims that the formula is accurate, while it is not.

Transformation of B_z if Q and q have different velocities

Let us treat a case where B_z is non-zero in the laboratory frame.

                     Q

                     ● ---> v

   

                 × × ×  B_z

                     • -------> V

                    q

                    m

The charge Q is positive and q negative. The magnetic field B_z points into the screen (marked with ×). We have, approximately:

       B_z  =  v / c  *  E_y.

We denote

       γ_V  =  1 / sqrt(1  -  V² / c²).

The acceleration of q is

       a_y  =  q / (γ_V m)  *  (V × B_z  +  E_y).

We switch to the comoving frame of Q.

https://en.wikipedia.org/wiki/Velocity-addition_formula

The velocity of q there is

       V'  =  (V - v) / (1 - v V / c²).

The acceleration of q in the comoving frame is

       a_y'  =  q / (γ_V' m)  *  E_y'.

The transformation of the acceleration is

       a_y'  =  a_y / ( γ²  (1  -   v V / c²)² ).

We obtain

       E_y'  =  γ_V' / γ_V  *  1 / ( γ² (1  -  v V / c²)² )

                    *  (V × B_z  +  E_y).  

It is a complicated formula. If v and V are slow, then, approximately:

       γ_V' / γ_V * 1 / (γ² (1 - v V / c²)²)

       =  1 + 1 / c²

           * (1/2 (V - v)² * (1 + 2 v V / c²)

               - 1/2 V² - v² + 2 v V)

       =  1 + 1 / c²  *  (-1/2 v² + v V)

       =  1 / γ + v V / c²,

where we dropped terms in which the velocities v or V appear in the third power. The result is approximately:

       E_y'  =  (1 / γ  +  v V / c²)  (E_y  -  V B_z)

                =  (1  -  1/2 v² / c²  +  v V / c²)

                    *  (E_y  -  V v / c * E_y).

We drop terms with 1 / c³ and obtain

       E_y'  =  E_y / γ.

This is also what Wikipedia predicts, as we saw in the section "A moving Q and a static q".

Transformation of B_x

Let us then check if the Wikipedia formula B_x'  =  B_x is correct.

                     ------>  B_x

                        • q    moves up from the

                                 screen at velocity V

    ^  y

    |

     ------> x

In the laboratory frame there is no electric field, just a magnetic field B_x.

The acceleration of q is

       a_y  =  q / (γ_V m)  *  V × B_x.

The acceleration in a frame moving at a velocity v to the positive x direction is

       a_y'  =  a_y / γ².

If we would believe the Wikipedia formulae, then E_y' = 0. Then

       a_y'  =  q / (γ_V' m)  *  V' × B_x',

where V' is the velocity of q in the moving frame. We obtain

       1 / (γ_V γ²)  *  V × B_x

       =  1 / γ_V'  *  V' × B_x'.

       =  1 / γ_V'  *  1 / γ  *  V × B_x'

   <=>

       B_x'  =  γ_V' / (γ_V γ)  *  B_x.

The formula B_x' = B_x is approximately correct.

The change in the inertia of q in the field of Q has a separate effect

In the calculations above, we ignored the change in the inertia of q in the electric field of Q. This is justified if the kinetic energy of q in various frames is much larger than the its potential energy in the field of Q.

If these energies are of the same order of magnitude, then it is easiest to do the calculations in the comoving frame of Q, and Lorentz transform the results to the desired frame. The concept of a Lorentz transformed electromagnetic field is not very useful then.

Conclusions

The Lorentz transformations of the electromagnetic field seem to be approximately correct in Wikipedia.

In practice, it is often better to use the Lorentz transformation of an acceleration, rather than transform E and B.