Intuitively, Γkij measures how much a vector pointing to a coordinate direction i changes to the k direction when the vector is parallel transported "one unit distance" to the j direction.
R₀₀ in a gravitational wave
Chris Hirata (2019) calculated the average R₀₀ for a gravitational wave of the h₊ polarization in the TT gauge.
We want to analyze what contributes to the 00 component of the Ricci tensor R in the case of a gravitational wave. The coordinates t, x, y, z are numbered 0, 1, 2, 3. The gravitational wave perturbation of the metric is a sine wave h₊:
g =
-1 0 0 0
0 1 + 2 h₊ 0 0
0 0 1 - 2 h₊ 0
0 0 0 1,
where
h(t, x, y, z) = ε * sin(ω t - x / λ),
and ε > 0 is very small.
The 00 component of the Ricci tensor R is
R₀₀ = R⁰₀₀₀ + R¹₀₁₀ + R¹₀₂₀ + R³₀₃₀
in terms of the Riemann tensor R. Let us study R¹₀₁₀.
1 B
--------------
| |
| |
--------------
A 2
^ t
|
------> x
An observer carries a vector, originally pointing to the time direction t, along two alternative routes from A to B, either going through 1 or 2, and measures the difference of the carried vectors at B.
The derivative of the metric component g₁₁ differs along the two routes.
Chris Hirata (2019) calculated above the values of the Christoffel symbols. The Ricci tensor component:
R¹₀₁₀ = dΓ¹₁₀ / dt
+ ...
The value Hirata calculated for R₀₀ is:
where the two last terms cause the average of R₀₀ to be negative. Let us explain where they come from.
Imagine a second square and a second observer placed on the right side of the diagram above. The first observer carries a vector of the form (a, b, 0, 0) from 2 to B, where a ≈ 1 and 0 < b is very small. Since the x metric changes between 2 and B, the value of b slightly changes.
But the second observer carries a vector (1, 0, 0, 0) from 2 to B. The contributions of the first and the second observers do not "cancel" each other for the line 2 to B! This is the reason why a Gauss-Bonnet-like theorem is not true for R₀₀. The sum of contributions for many adjacent loops is not the same as the contribution of the large loop which encloses the small loops.
Now we have the explanation for the counterintuitive fact that a wave metric g has R₀₀ which, on the average, differs from 0.
Note that static test masses placed initially at fixed coordinates (x, y, z) stay at those coordinates. There is no "focusing" of the test masses even though the average R₀₀ differs from zero!
Conjectures
Definition. Focusing of initially static test masses in a spatial volume V: the test masses start at fixed spatial coordinate positions in V at the same coordinate time, and their coordinate velocity is initially zero. Let D be the density of test masses per cubic meter, where the volume is measured in proper distances. There is focusing if
d²D / dt² < 0,
where t is the coordinate time.
Conjecture 1. If the Ricci tensor R = 0 everywhere, then there is no focusing or defocusing of initially static test masses.
We used Conjecture 1 in our June 17, 2024 blog post where we showed that the Einstein field equations do not allow the existence of gravitational wave packets. The gravity of a wave packet focuses initially static test masses, but R = 0 inside the wave and outside it. This is a contradiction.
Conjecture 2. If R₀₀ ≥ 0 everywhere, then there is focusing of initially static test masses. If R₀₀ ≤ 0 everywhere, then there is defocusing.
Conjecture 3. Let us start from the Schwarzschild interior and exterior solution for a spherical mass M. However we change the metric g inside M, the integral of the Ricci scalar R, weighed by the "volume element" of the Einstein-Hilbert action, over M and its immediate neighborhood, does not change.
We are not sure if Conjecture 3 is true. Its intention is to say that a "total curvature" does not change inside M when the metric g does not change outside M.
The total curvature comes from the mass density, the pressure, and possible gravitational waves inside M.
Conjecture 3 implies a conservation law for "energy", which includes also gravitational waves.
Conjecture 3 implies that the Ricci scalar R cannot be zero for gravitational waves. The waves are never solutions of the full Einstein field equations.
Proof sketch of Conjecture 1: failure
UPDATE July 18, 2024: the proof sketch does not work. If the metric of x, y, z has a negative curvature, then the test masses will disperse faster than in euclidean space. If we put a focusing effect to the metric of time by slowing down time in the middle of the wave packet, we can make R₀₀ zero, but still focus initially static test masses, because the metric of time focuses them.
However, does this necessarily make R₁₁ or R₂₂ or R₃₃ non-zero?
----
^
|
• •
• • • •
<-- • • × P • -->
• • • •
• •
| C = cloud of dispersing
v test masses m
Let us try to prove Conjecture 1.
We assume that the geometric definition in Wikipedia holds: R₀₀ at a point P = (t, x, y, z) tells us how fast test masses m sent at low velocities from P disperse. A zero curvature means that the proper volume of the test mass cloud C grows just like it would grow in euclidean space.
Let the metric be g.
Let us assume that the entire volume of space at some time coordinate t₀ is filled with distinct (i.e., intersections are empty) clouds C of dispersing test masses sent from various points P.
For each test mass m at (t₀, x, y, z), we assume another test mass m' at the same point, but whose coordinate velocity is zero. For each cloud C, we obtain a cloud C' of initially static test masses.
Assumption. The metric g does not make the clouds C' to intersect for some time after t₀.
The Assumption is true for the sine gravitational wave, because test masses m' stay at fixed coordinate positions. The Assumption probably is true for sufficiently "well behaved" metrics g.
Since the clouds C' fill the entire volume of space, and there is focusing, there has to be a cloud C' whose volume V' has a negative second time derivative d²V' / dt² at t₀.
Conjecture 4. If C' has d²V' / dt² < 0, then the volume of the corresponding cloud C has to grow slower than C would grow in euclidean space. That is, R₀₀ > 0 for the point P of the cloud C.
Conjecture 4 should be true at least for sufficiently "well behaved" metrics g. No, it is not true! See the UPDATE we wrote above.
A method of making R₀₀ zero in a metric, but still focusing initially static test masses
Let us make the spatial metric such that it has negative curvature. It is "saddle-shaped". If we send test masses from a spacetime point to all spatial directions, the volume of the test mass cloud grows faster than in euclidean metric. That is, R₀₀ < 0.
We can then reset R₀₀ to zero by making time to flow slower near the center of the system. This focuses test masses and can cancel tge negative R₀₀.
If we have initially static test masses, they are pulled toward the center by the slower flow of time there. Thus, the system does focus initially static test masses, even though R₀₀ = 0.
A gravitational wave in the TT gauge has an undulating spatial metric. Apparently, the saddle shape (negative curvature) dominates there over the spherical shape (positive curvature). This explains how, on the average, R₀₀ < 0.
One could try to reset R₀₀ in a wave packet to zero by making time to flow slower at the center of the wave packet. We are not sure if this can succeed.
Also, one could try to make R = 0 in the packet, just like the Einstein field equations require.
The paper in the link states that exact wavelike solutions for the Einstein field equations are known only for some unnatural, symmetric configurations.
Our own work in June 2024 with rogue variations revealed that general relativity has no solutions at all for "dynamic systems". Thus, it is hopeless to try to find an exact solution which also includes the source that produces the wave.
A gravitational wave packet must have R₀₀ zero but focus initially static test masses => then the energy density can be calculated with the method above
Let us have a spherically symmetric mass M. If M would be static, then the metric g around M would have the Ricci tensor R zero. In particular, R₀₀ is zero.
Let us then imagine that we make M to oscillate back and forth. Then M produces a gravitational wave, which is kind of a "retarded" field which cannot fully keep up with the accelerated movement of M.
It might be that the retarded field has the Ricci tensor R zero, just like the static field of M.
If a gravitational wave packet carries a mass-energy m, we expect it to pull test masses toward itself just like any mass of m. We conclude that the wave must focus intially static test masses.
Let us assume that the linearized Einstein equations give an approximate form for a gravitational wave packet, except that R₀₀ fluctuates while it should not.
Chris Hirata (2019) calculated R₀₀ for a sine wave.
We can make R₀₀ approximately zero by modifying the metric of time in such a way that we put a "negative mass density" at those locations of the wave where R₀₀ > 0, and a "positive mass density" at locations where R₀₀ < 0. The added masses will travel at the speed of light.
If the new metric with added masses approximates a real gravitational wave packet, then the Chris Hirata (2019) method of calculation really gives the energy density of a gravitational wave.
There are a lot of assumptions in the reasoning above. If they happen to be correct, then we have an explanation for the energy density of a gravitational wave.
Our reasoning did not use the full Einstein field equations at all. The following are enough:
1. the field around a spherical mass M is approximately Schwarzschild; in particular, the stretching of the spatial metric is like in Schwarzschild;
2. when M is oscillated, the retarded field forms a gravitational wave, and the retarded field inherits the property R₀₀ = 0 from the static field;
3. the spatial metric of the retarded field is approximately what we get from the linearized Einstein equations; we probably can derive the metric also without using any Einstein equations, by just considering retardation of the field;
4. the metric of time in a wave packet is like for an electromagnetic wave packet of the same mass-energy E.
Note that above, the metric of time reveals the energy content of a gravitational wave to observers. The spatial metric is what actually carries the energy: we can extract the energy by using the fact that the wave stretches proper distances.
A gravitational wave must not shorten proper distances if it does slow down time as much: otherwise, we get superluminal communication
In this blog we have remarked that if a gravitational wave would shorten proper distances, and not slow down time enough, then the coordinate speed of light would exceed the speed of light in the underlying Minkowski space.
We cannot accept superluminal communication. Therefore, the metric η + h₊ produced by the linearized Einstein equations cannot be the correct metric.
Could it be that the energy density of a wave packet slows down time enough, so that the coordinate speed of light is not too fast? It does not look like that. The energy density is not large enough.
Note that in the static field of a spherical mass M, the spatial metric is always stretched, never contracted.
In our earlier blog posts, we speculated that the stretched spatial metric in a gravitational wave comes from energy shipping in an underlying field which is analogous to an electromagnetic wave.
Conclusions
We finally found a possible explanation for the fact that R₀₀ calculated from a sine gravitational wave gives the energy density of the wave.
A gravitational sine wave derived from the linearized Einstein equations has R₀₀ < 0, but its Ricci scalar R = 0. By adding the wave metric perturbation to the interior Schwarzschild solution we can reset R₀₀ to zero locally. But we cannot reset R. This suggests that gravitational wave packets always have R > 0, which reflects the fact that they carry energy.
Conjecture. A gravitational wave packet has R₀₀ = 0, but R > 0.
The sine wave has both R₀₀ and R₃₃ negative because the metric to the x and y directions is negatively curved, "saddle-shaped". A narrow conical beam of geodesics to the t or z direction spreads out faster than in euclidean space.
We have to check what the Einstein-Hilbert action says about this conjecture.
We have to think about waves which only stretch, not shorten, proper distances. How to model them?




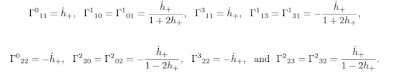

No comments:
Post a Comment