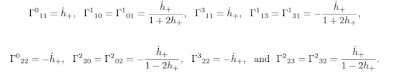UPDATE August 3, 2024: We cannot use an infinitesimal variation to slow down time by dt as explained below. The problem is that if we try to "glue" the time-translated part of the history to the part which is stretched by dt, the gluing point will have a discontinuous time derivative of the metric g.
That is, if one wants to displace a segment of a sine wave a little bit, then gluing it to the old wave makes the derivative discontinuous. A discontinuous derivative of a metric may mean, for example, matter of infinite density at the point of discontinuity.
We have to check what happens if we do the gluing at the birth place of a gravitational wave.
See our blog post August 4, 2024. Our claim below is correct: there is no history where a gravitational wave is generated. But the proof is a bit different.
----
What implications does the speed limit have on the variation?
An example: some of the mass M suddenly disappears
This is our favorite example of fooling the Einstein field equations. The system M is a static spherically symmetric mass. Then we use a magic trick to make some of the mass disappear suddenly. Let us denote the new mass by
M' < M.
We assume weak fields.
If we were allowed to alter the metric g infinitely fast, then we could adjust the metric to that Schwarzschild metric which satisfies the field equations for the reduced mass M'. But we cannot do that.
Let us try to find a stationary point of the Einstein-Hilbert action S for this example.
ρ
### r ● r ###
shell M' shell
^ y
|
-----> x
Let us imagine that we right now have a metric g which matches the mass M' at the center, and g also matches an imagined spherical shell of a mass M - M' at some radius r from the center. The shell does not have any matter, because the matter disappeared through magic, but the metric g is adjusted as if there were matter there.
The shell is not thin. The Ricci tensor R for the shell is obtained through trace reversing the mass stress-energy tensor T, which only contains the mass density ρ of the shell as its 00 component:
R =
ρ / 2 0 0 0
0 ρ / 2 0 0
0 0 ρ / 2 0
0 0 0 ρ / 2,
and the Ricci scalar is:
R = ρ.
The metric g has the diagonal almost (-1, 1, 1, 1) because the field is weak. The metric has g₀₀ slightly larger than -1, and the x coordinate metric g₁₁ slightly larger than 1.
The Wikipedia formula gives:
δR = R₀₀ * -δg₀₀,
δR = R₁₁ * -δg₁₁,
and so on.
If we make g₀₀ larger, that is, slow down time, then δR is negative. Also,
sqrt(-det(g))
in the action S formula becomes smaller. Thus, the metric g is not a stationary point of the action S. We can increase g₀₀, and S declines linearly with g₀₀.
Can we make R = 0 simply by slowing down time? Hardly. Various components of R depend in a complex way on g₀₀.
Replacing the shell with gravitational waves which carry the mass-energy M - M' away
If it is possible to find a metric which describes a realistic gravitational wave, and where R = 0, then we do not need a magic trick in the example above. A spherical gravitational wave front carries the mass-energy M - M' away. The Ricci tensor is everywhere zero outside M'.
However, we can ban gravitational wave solutions by demanding that the metric has to be perfectly symmetric. There are no longitudinal gravitational waves.
Ivor Robinson and Andrzej Trautman (1960) found spherical wave solutions of the Einstein field equations. Let us look at their metric:
The wave equation is:
The authors say that in the linear approximation they have waves whose wave fronts are at
σ = constant.
Apparently,
σ = r - c t,
using more familiar coordinates, r for the radius and t for time.
The authors write that if they choose K > 0, then there is a "singularity" on each wave front, which "might represent a flow of energy" to the wave, so that energy does not run out when the wave carries it away.
The description is very far from a practical gravitational wave whose source would be a binary star. The authors neither mention anything about the metric change when the central mass M loses mass-energy in gravitational waves.
A spherically symmetric metric of time plus a shell of gravitational waves makes R ≠ 0 inside the gravitational waves
Proof sketch. We assume that the metric of time, g₀₀, is spherically symmetric. We assume that the mass-energy of a gravitational wave pulls test masses just like the mass-energy of matter does.
M - M'
### ● ###
shell M' shell
The central mass M' radiated away the mass M - M' in a shell of gravitational waves.
Let us have initially static (static in the coordinates) test masses m. Outside the shell, they feel a gravitational pull which is relatively larger than inside the shell. Therefore, test masses will become denser at the shell. Thus,
R₀₀ > 1,
inside the shell, unless the spatial metric can cancel the focusing effect of the metric of time.
^
|
•
<---- • × • ----> ● M'
• m
|
v
##############
shell
M - M'
Let us consider test masses m sent from inside the shell from one static point, at low velocities to every direction. The cloud of test masses will have a smaller volume than in euclidean space, if we just consider the metric of time. The mass-energy density of the gravitational wave pulls the test masses together.
Let us reset R₀₀ to zero by making the spatial metric saddle-shaped, that is, the average spatial curvature is negative. Then the volume of the cloud of test masses is surprisingly large: that can cancel the focusing effect of the metric of time.
Let us then send a tight cone of geodesics to a spatial direction where the spatial metric has a negative Ricci curvature. Since the spatial metric overall has a negative curvature, such a direction must exist. Can we use the metric of time to cancel the negative Ricci curvature in that direction?
We can probably ignore the field of M' altogether, because its field has the Ricci tensor R = 0 outside M'.
^ g₀₀
|
| __--------------------
| ___----
-1
P
###
shell
r <------ M'
Let us then look at the metric of time g₀₀ created by the shell. At some r inside the shell, we have a point P where
d²g₀₀ / dr² < 0.
spatial
direction
^
| \ / geodesics
| \ / s
| \ /
| × P start point
--------------------------> t
Let us send a cone of geodesics from P to a spatial direction where the spatial Ricci curvature is negative.
As the cone of geodesics to a spatial direction opens up, its "diameter" in terms of time changes according to g₀₀. Let s be the spatial distance from the start point P. We have:
d²g₀₀(s) / ds² < 0.
The metric of time adds to the negative Ricci curvature into the spatial direction. We cannot use the metric of time to cancel a negative Ricci curvature to the spatial direction.
It could still be that if the metric of time is not spherically symmetric, we might be able to cancel the negative Ricci curvature to the spatial direction.
Conjecture 1. If a central mass M magically loses a mass M - M', or radiates it away as gravitational waves, then the Ricci tensor R cannot be zero outside the remaining central mass M'.
The mass-energy density of a sine gravitational wave packet in nature is its Ricci scalar -R / κ?
Chris Hirata (2019) calculated the Ricci tensor R of a sine gravitational wave
g = η + h₊,
and noticed that the Ricci scalar R for it is zero. He derives the mass-energy density by determining what kind of a stress-energy tensor T produces R in the Einstein field equations. The component
R₀₀ = κ T₀₀
has a negative mass-energy density T₀₀. Hirata assumes that -T₀₀ is the energy density carried by the gravitational wave. Here,
κ = 8 π G / c⁴
is the Einstein constant.
Let us have a gravitational wave packet g which inside the packet is roughly a sine wave.
Let us "correct" the wave packet metric g by superposing the temporal (time) metric perturbation of mass-energy of the density -T₀₀ moving at a speed of light along with the wave packet. In this way, we increase R₀₀ to zero for the new metric g'.
Now we have a new metric g', for which the the Ricci scalar R is
R = κ T₀₀.
The energy density is
-R / κ.
For mass-energy of matter with no pressure, we have the energy density
R / κ.
Is this reasonable? Could this be a stationary point of the Einstein-Hilbert action S if we take into account that faster-than-light signals are not allowed?
Superposing a matter wave (electromagnetic wave) on a gravitational wave packet
Chris Hirata calculated that the R₀₀ Ricci tensor component in a sine gravitational wave is:
Let us for a while forget about the oscillation of R₀₀ between positive and negative values. We will analyze that later.
We assume weak fields. The metric is
g = η + h =
-1 0 0 0
0 1 + 2 h₊ 0 0
0 0 1 - 2 h₊ 0
0 0 0 0,
where |h₊| is very small and h₊ describes a sine wave.
Let us denote
R₀₀ = -κ ρ.
The Ricci tensor R of a sine gravitational wave is approximately
R =
-κ ρ 0 0 κ ρ
0 0 0 0
0 0 0 0
κ ρ 0 0 -κ ρ.
The Einstein tensor G is the same as R because the Ricci scalar R is approximately zero.
The stress-energy tensor T which corresponds to G is approximately
T =
-ρ 0 0 ρ
0 0 0 0
0 0 0 0
ρ 0 0 -ρ.
The stress-energy tensor T which corresponds to a particle moving at the speed of light is
where
Chris Hirata in his paper has the speed of light c set to 1, as well as Newton's gravity constant.
Let us superpose matter moving at the speed of light onto the sine gravitational wave.
If we have a mass-energy density ρ moving to the z direction at the speed of light, then its stress-energy tensor is:
T' =
ρ 0 0 ρ
0 0 0 0
0 0 0 0
ρ 0 0 ρ.
Let us trace reverse T'. We obtain
R' =
κ ρ 0 0 κ ρ
0 0 0 0
0 0 0 0
κ ρ 0 0 κ ρ.
Let
η + k
be the metric whose Ricci tensor is R' (does such a perturbation exist?).
Can we assume that the Ricci tensor R is approximately linear in perturbations of the metric? If yes, then the Ricci tensor for
g'' = η + h + k
is approximately
R'' =
0 0 0 2 κ ρ
0 0 0 0
0 0 0 0
2 κ ρ 0 0 0,
and the Ricci scalar R'' is approximately zero, assuming that g'' is approximately orthogonal.
We found a metric g'', for which the variation of the Einstein-Hilbert action S is approximately zero! Since the off-diagonal corner elements of R'' are different from zero, this is not a solution of the full Einstein field equations, but it is an almost stationary solution.
Can we now use Noether's approximate theorem from our July 9, 2024 blog post to prove that energy is approximately conserved?
Noether's theorem DOES prove that energy is conserved for stationary points of the Einstein-Hilbert action S; but the next section proves that we do not have a stationary point
The claim in the headline of this section follows almost trivially if we assume that the start state and the end state are such that we can determine the energy of the system from the matter lagrangian LM alone and ignore gravity!
history,
gravitational waves
which get absorbed back
● --------------------------------------------- ●
start state end state
where energy where energy
well defined well defined
For example, the end and the start state might be static matter whose density is very low.
We assume that there exists metrics g, g' for the start and the end states.
We assume that we can obtain the Ricci tensor R for the metrics g and g' by trace reversing the stress-energy tensor. Then the Ricci scalar at a location is
R = κ ρ,
where κ is the Einstein constant and ρ is the mass density at the location.
In the Einstein-Hilbert action S for the history start and end states, the volume element sqrt(-det(g)) is almost exactly 1, and
1 / (2 κ) * R + LM = 1/2 ρ - ρ = -1/2 ρ.
At the start and end states, varying the the history of the system, as explained in the Wikipedia article about Noether's theorem, by dt at the start and -dt at the end must keep the action S constant. This implies that the integral of ρ over the entire space must be the same at the start and end states. That is, energy is conserved.
The same argument should work if the start and the end states are spherically symmetric spheres of incompressible fluid, just as in the Schwarzschild interior and exterior solutions.
Conservation of energy between the start and end states does not require us to assume anything more about the history between the states, except that there is a continuos time time symmetry which allows us to "shift" the middle part of the history by dt.
The middle part of the history can include gravitational waves which get absorbed back into the matter content M.
NOTE: No, it cannot! See the next section.
We, naturally, have to assume that there exists a stationary point of the action S. Our results with rogue variations may show that there is no stationary point?
Noether's time variation shows that the Einstein-Hilbert action does NOT allow gravitational waves?
oscillating masses
<--->
●\/\/\/● variation: before emitting
the wave, speed up
everything by dt
---------- quadrupole wave
---------- packet, R = 0
----------
----------
---------- variation: slow down
everything by dt
The experiment:
1. Initially, the oscillating masses are static. Let their mass-energy be M.
2. The masses then oscillate, and radiate a large amount of the energy of the system away in a gravitational wave pulse. Let the metric be g.
3. The masses are again static at the end of the process. The remaining mass-energy is M' < M.
The Noether time variation:
A. Before emitting the waves, we "speed up time" by dt.
B. When the wave packet is receding from the system, we "slow down time" by dt.
Since M > M', the action S of the mass system has a non-zero change when A and B are applied. This is because in LM, the "potential energy" is larger at A than at B.
But the change to S from the gravitational wave packet at B is zero because the Ricci tensor R is zero and:
The "slowing down of time" by dt can be done by changing the metric g of the gravitational wave infinitesimally. The formula above from the Wikipedia article about the Einstein-Hilbert action says that the Ricci scalar R stays zero in the variation. The integral of R over the wave packet stays zero.
Assumption. In the formula for δR above, we have to assume that the error term, which is of the form ~ (δg^μν)², "behaves well" and the integral of the error over the entire wave packet is ~ dt², when we slow down time by dt. Also, the variation must be well approximated as the sum of individual variations of each gμν.
We showed that the action S changes in an infinitesimal variation of the metric g. Thus, g is not a stationary point of the action. The Einstein-Hilbert action has no solution for an experiment where a gravitational wave packet is generated.
Let us still check that the Einstein field equations really have to hold in this experiment. Could it be that the light-speed limit of signals spoils the derivation of the Einstein field equations in the Wikipedia article?
The contradiction which we derived shows that a lagrangian density is not allowed to "hide" energy. The energy visible at the start of the experiment must be visible in the lagrangian at all times. One is not allowed to sweep it under the rug. The contradiction also shows that our result above, about energy conservation in the Einstein-Hilbert action is void if there are gravitational waves: there is no stationary point of the action S at all.
The lagrangian density of electromagnetic waves: if we treat B as a "dependent" field from E, then it can handle electromagnetic waves
In the preceding section, we slowed down a packet of gravitational waves by a time dt. We cannot speed them up by dt, because then the signal would propagate faster than light. Or could we allow such an infinitesimal breach of the light speed limit?
Let us check what people say about the electromagnetic lagrangian and electromagnetic waves. We cannot find anything in the literature.
If the system is, as in the preceding section, such that it does not contain any light-speed waves in a certain period of time, then we can "speed up time" by dt during that period, and "slow down time" by dt when a wave is propagating.
(Jim Branson, 2013)
In electromagnetism, the lagrangian density for the electromagnetic wave does not "hide" its energy?
If we slow down time, the "kinetic" part B² of the wave should be reduced. Does that happen? If B is not treated as an independent field, but is born from the electric field through the formula
B ~ dE / dt,
then B² really is reduced as time is slowed. It is like a vibrating string: if we slow down time, the kinetic energy of the string is reduced.
For a metric g, we do not have a similar division of which part of the field is "dependent". That is why the Einstein-Hilbert action cannot handle a gravitational wave.
Linearized Einstein equations would work better, because they probably have properties which are analogous to electromagnetism.
Conclusions
Let us close this long blog post.
We derived a very important result: the Einstein Hilbert action does not have a stationary point for a gravitational wave packet. That is, general relativity does not allow gravitational waves to exist – even though we have observed in nature such waves.
The reason for the failure is that the Ricci tensor R is zero in a wave, and "hides" the energy of a wave.
Fixing the problem would require making general relativity more analogous to electromagnetism, so that we can separate the "kinetic part" (B²) of the lagrangian density.
A sine gravitational wave derived from the linearized Einstein field equations has certain components of R non-zero. It may behave more reasonably than a R = 0 wave if we "slow down time" by dt.
Above we have the energy density of a sine gravitational wave, calculated by Chris Hirata (2019). The density is ~ square of the time derivative of the metric perturbation h₊. This is reasonable, just like 1/2 m v² is the kinetic energy of an oscillating string.
It is not clear if the light-speed limit on signals affects the variational calculus at all. We might even allow infinitesimal breaches of the limit in variations, though not in histories themselves.
We did not yet get more insight into why the average stress-tensor component -T₀₀ gives the correct energy density of a gravitational wave occurring in nature.