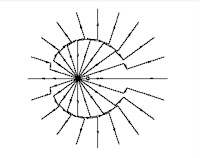
In the diagram we have the electric lines of force for a charge which was suddenly moved to the left. The lines are kept non-breaking by a magnetic field which varies with time.
Ricci curvature R₀₀ = 0 means that the lines of force must not break
Having the Ricci curvature R₀₀ = 0 (the curvature to the time direction) means that a cube of test masses m, which are initially static, must preserve its volume when the masses are let to float freely.
The movement of test masses is like a flow of incompressible liquid. The lines of force acting on the test masses must not break – otherwise the density of test masses would not stay constant. The vector field defined by the electric field E must be "sourceless", or solenoidal.
Is it so that gravitomagnetism has to be exactly analogous to ordinary magnetism? Yes, for single accelerating masses there can be no factor 4
Newtonian gravity and its lines of force look exactly like the Coulomb force. Let us assume that retardation of gravity is identical to the electric force. Let us also assume that weak gravity fields obey Gauss's law.
Then a good hypothesis is that gravitomagnetism acts on test masses exactly like magnetism acts on test charges.
In our November 13, 2023 we presented a hypothesis that gravitomagnetism is exactly analogous to magnetism. We have here more evidence that supports that hypothesis.
However, we must note that the energy density of a gravitational wave is 16 times the analogous electromagnetic wave. Changes in the spatial metric seem to carry this large energy density. The gravitomagnetism which we consider in this blog post concerns the metric of time. The metric of time produces the newtonian gravity force.
A. Barros (2016) writes that for weak fields, the Kerr metric is exactly analogous to the electric and magnetic field of a spinning charge. The lagrangian is identical.
On August 7, 2023 we wrote that in the literature, the gravitomagnetic field of a spinning mass is claimed to be 4-fold compared to the analogous spinning electric charge. Is this possible? What happens in electromagnetism if we make the magnetic field 4-fold?
If there would just be retardation and no magnetic field would exist, then in the diagram, the electric lines of force would break at the circle.
A changing magnetic field is able to connect the ends of the lines of force through the formula:
If we make B 4-fold, then the electric field along the circle will be too strong. We end up with too many lines of force along the circle.
The gravitomagnetic field for a moving single mass cannot be 4-fold relative to the analogous magnetic field of a moving single charge.
In this example, the gravitomagnetic field is already "detached" from the point mass which generated it. The field of slowly moving masses may be quite different from the field of a rapidly accelerated mass.
What about "current loops"? A rotating mass is a "loop" of a mass current. Could it be that a loop somehow has a 4-fold gravitomagnetic field?
That would be strange. How would nature know which movement of an atom constitutes a mass current loop?
The spatial metric around a static spherical mass shell cannot be calculated by summing metric perturbations for each atom, as we have noted in this blog. Could it be that there is a similar nonlinear effect which radically changes the gravitomagnetic effect of a rotating mass shell?
Using the Einstein approximation formula to calculate the gravitomagnetic effect of a sphere
The strange factor 4 in the literature probably originates from calculations of Josef Lense and Hans Thirring in 1918. They defined a metric which is a weak field approximation of the Kerr metric.
On May 29, 2024 we showed that no rotating mass M can have a metric which solves the Einstein field equations. Therefore, we cannot define what is the "correct" metric around a rotating mass in general relativity. Anyway, we have to check how Lense and Thirring got the factor 4.
Claus Lämmerzahl and Gernot Neugebauer (2001) give an elementary derivation of the Lense-Thirring metric. They seem to apply the Einstein approximation formula (see the blog post August 16, 2023) to the metric tensor, including the mass flow in the rotating body:
where the "frame-dragging" off-diagonal component is:
in the metric:
Let us analyze this. How does the factor 4 come about?
Let us have a mass circle which rotates around its center. Below we have drawn two elements dm of the circle. We calculate what the Einstein approximation formula says.
We assume weak fields.
^ v
\ \
× dm
\ center
dm r = radius
α = angle(center-dm, x axis)
^ y
|
-----> x
^ V
|
• m test mass (0, -y)
We assume that dm = dα. Then the mass of the entire circle is 2 π and its angular momentum L = 2 π v r. The coordinates of the circle center are (0, 0) and the test mass m (0, -y).
In the diagram, the contribution of the two elements dm to the t, x component of tilde-g₁ at the test mass m is κ c² times:
dm sin(α) v / (y - r sin(α))
- dm sin(α) v / (y + r sin(α))
≈ dα sin(α) v * 1 / y * 2 r / y * sin(α)
= 2 v r / y² * sin²(α) dα.
The integral of sin²(α) from 0 to π is π / 2. The contribution of the full circle is
κ c² π v r / y²
= 8 π G / c² * π v r / y²
= 4 π G / c² * L / y²
The formula we obtained is totally different from the one in the paper. Strange. Maybe the authors have set 8 π / c² = 1?
Anyway, let us continue our calculation. The Einstein approximation formula indicates that the metric g at the test mass m is something like
g =
≈ -1 4 π G / c² * L / y² 0 0
4 π G / c² * L / y² ≈ 1 0 0
0 0 ≈ 1 0
0 0 0 ≈1,
in cartesian coordinates t, x, y, z. What is the strength of magnetic gravity there?
Let us use the geodesic equation to determine the x acceleration of a test mass m which approaches the circle at a velocity V. In the formula above, s is the proper time τ of the test mass.
We want to determine
d²x / dτ² = -Γ¹₀₀ * dt / dτ * dt / dτ
- 2 Γ¹₀₂ * dt / dτ * dy / dτ
- Γ¹₂₂ * dy / dτ * dy / dτ
= -Γ¹₀₀ - 2 Γ¹₀₂ V - Γ¹₂₂ V².
Γ¹₀₀ = 1/2 g¹⁰ (0 + 0 - 0)
+ 1/2 g¹¹ (0 + 0 - 0) = 0,
Γ¹₂₂ = 1/2 g¹⁰ (0 + 0 - 0)
+ 1/2 g¹¹ (0 + 0 - 0) = 0,
Γ¹₀₂ = 1/2 g¹⁰ (0 + dg₀₀ / dy - 0)
+ 1/2 g¹¹ (0 + dg₀₁ / dy - 0)
≈ 1/2 dg₀₁ / dy.
On the last line we use the fact that both g¹⁰ and dg₀₀ / dy have very small absolute values and their product is negligible, and that g¹¹ ≈ 1. We then have:
d²x / dτ² = -V * d (4 π G / c² * L / y²) / dy
= V * 8 π G / c² * L / y³.
The gravitomagnetic force on the test mass is
Fgm = m V * 8 π / c² * G * L / y³.
Let us compare this to the magnetic field of a electrically charged rotating sphere. The magnetic dipole moment m of a solid, uniformly charged sphere is
m = 1/2 Le,
where Le is the "charge angular momentum" of the sphere, defined analogously with the mass angular momentum:
Le = Σ qi v r.
i
In the equatorial plane, the magnetic field of the rotating sphere is:
B = μ₀ / (4 π) * m / y³
= 1 / (8 π ε₀ c²) * Le / y³.
The magnetic force on a test charge q is:
Fem = q V * 1 / 2 * 1 / c²
* 1 / (4 π ε₀) * Le / y³.
The gravitomagnetic force is 16 π times the analogous magnetic force. This does not make sense. The Einstein approximation formula produces wildly wrong results.
The gravitomagnetic effect of a moving cylinder in general relativity: the factor 4 comes up here
On April 26, 2024 were able to solve an approximate metric around a long uniform cylinder, from the Einstein field equations. Let us use our result to derive the path of a test mass which approaches the cylinder obliquely. If we imagine that the cylinder is moving and the test mass approaches it along a normal, then we also have calculated the gravitomagnetic effect in general relativity.
z ρ = mass / length
---> =============== static long cylinder
|
v r Vr
^ ^ V
| /
| /
• ---> Vz
m
test mass
The cylindrical coordinates are t, r, φ, z.
We derived:
dg₁₁ / dr = r d²g₀₀ / dz²
≈ 0.
If the cylinder is very long, then |d²g₀₀ / dz²| is very small, and we can assume that the metric component g₁₁ does not depend on r.
On April 28, 2024 we derived:
dg₃₃ / dr = dg₀₀ / dr + r d²g / dz²
≈ dg₀₀ / dr.
Let us assume that the test mass m is near the midpoint of the cylinder. Then off-diagonal components in the metric g are very small and can be neglected.
The metric of time g₀₀ (which is close to -1) is calculated from newtonian gravity:
dg₀₀ / dr = -2 G m ρ / r * 1 / (m c²)
= -2 G / c² * ρ / r,
where ρ is the mass of the cylinder per length. Note that dτ² = g₀₀ dt², from which the factor 2.
We use the geodesic equation again:
If we assume that
|V| << c.
Then
d²z / dτ² = -Γ³₀₀ dt / dτ * dt / dτ
- 2 Γ³₀₁ dt / dτ * dr / dτ
- Γ³₁₁ dr / dτ * dr / dτ
- 2 Γ³₀₃ dt / dτ * dz / dτ
- 2 Γ³₁₃ dr / dτ * dz / dτ
- Γ³₃₃ dz / dτ * dz / dτ.
The Christoffel symbols:
Γ³₀₀ = 1/2 g³³ (0 + 0 - 0),
Γ³₀₁ = 1/2 g³³ (0 + 0 - 0),
Γ³₁₁ = 1/2 g³³ (0 + 0 - 0),
Γ³₀₃ = 1/2 g³³ (0 + 0 - 0),
Γ³₁₃ = 1/2 g³³ (dg₃₃ / dr + 0 - 0),
Γ³₃₃ = 1/2 g³³ (0 + 0 - 0).
We obtain:
d²z / dτ² = -dg₃₃ / dr * -Vr * Vz
= -Vr Vz * 2 G / c² * ρ / r.
The proper time τ of the test mass m slows down as it descends closer to the cylinder. Let us calculate the effect. The slowdown is due to two things:
1. the metric of time |g₀₀| is slower close to the cylinder, and
2. the velocity of the test mass grows close to the cylinder, which slows down its proper time.
Item 1:
Let m approach the cylinder for a unit time. The rate dτ / dt (≈ 1) slows down by
Vr G / c² * ρ / r,
which translates to a z acceleration:
-Vr Vz G / c² * ρ / r.
Item 2:
The effect is as large as for item 1:
-Vr Vz G / c² * ρ / r.
The combined effect of all of the above is
-Vr Vz * 4 G / c² * ρ / r.
We finally found a possible origin of the strange factor 4 in the literature!
A half of the effect is due to the stretching of the z metric g₃₃ close to the cylinder. One fourth comes from the slowdown of time close to the cylinder. One fourth comes from the increased kinetic energy. Are these really "magnetic" effects?
The analogue between gravity and electromagnetism, in the case of a moving cylinder and a test charge approaching it
ρ = charge / length
================== --> Vz
cylinder
^
|
• q test charge
The "electric field":
Gravity:
Eg = G ρ / r.
Electromagnetism:
E = 1 / (4 π ε₀) * ρ / r,
where ρ is the charge per length.
The "magnetic field":
Gravity:
Bg = 4 Vz / c² * Eg.
Electromagnetism:
B = Vz / c² * E.
A test mass moving along a moving cylinder
Let us check if the analogue extends to other movements than a normal movement.
============ static cylinder
•---> Vz
d²r / dτ² = -Γ¹₀₀ dt / dτ * dt / dτ
- 2 Γ¹₀₁ dt / dτ * dr / dτ
- Γ¹₁₁ dr / dτ * dr / dτ
- 2 Γ¹₀₃ dt / dτ * dz / dτ
- 2 Γ¹₁₃ dr / dτ * dz / dτ
- Γ¹₃₃ dz / dτ * dz / dτ.
The three last terms are associated with the velocity
Vz = dz / dτ,
and can create a "magnetic" force. We can discard the one with the dr / dτ factor.
Γ¹₀₃ = 1/2 g¹¹ (0 + 0 - 0),
Γ¹₃₃ = 1/2 g¹¹ (0 + 0 - dg₃₃ / dr)
= -1/2 g¹¹ d(-2 G / c² * ρ / r) / dr
≈ -G / c² * ρ / r².
Then
d²r / dτ² = Vz² * G / c² * ρ / r².
The associated force is proportional to the square of the velocity Vz. It is not a "magnetic" force.
Let us assume that the cylinder moves to the right at a very slow speed v. This simulates an electric current, which moves very slowly inside a wire.
========== --> v
• ------> Vz
A "magnetic" force arises:
d²r / dτ² = 2 Vz v * G / c² * ρ / r².
But depends on 1 / r², not on the "electric" field which is ~ 1 / r.
We cannot find anything which would resemble electromagnetism. Thus, gravitomagnetism makes no sense for a movement parallel to the cylinder.
Conclusions
For a moving cylinder, there is not a good analogy with magnetism in general relativity.
If we look at a "free" gravity field, it would be nice to have a mechanism which imitayes the magnetic field, in order to preserve Gauss's law.
We will write another blog post about the gravitomagnetic field of a rotating mass. It is not clear to us what kind of a magnetic force is natural for general relativity. Is the Kerr metric natural?
In our own Minkowski & newtonian gravity model, gravitomagnetism is not yet clear, either.





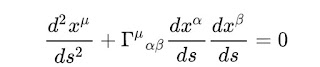




No comments:
Post a Comment