https://en.wikipedia.org/wiki/Einstein%E2%80%93Hilbert_action
The "lagrangian" inside the action is strange: the "energy" of the Ricci scalar R is either negative potential energy, or kinetic energy, since the sign of R is the same as kinetic energy in LM. The signs go like this:
∫ (R - V) * sqrt(-det(g)) * dx⁴,
where the Ricci scalar R is positive and the positive potential energy of the lagrangian LM is V. In most cases, V is predominantly the energy of the mass M in the system.
The lagrangian for a static system is not about the minimization of potential energy. Rather, it is like a lagrangian of a dynamical, moving system with both kinetic and potential energy. The task is to find a path which gets the "dynamics" right.
We have been interested in how the Einstein-Hilbert action reacts in case a "charge", like a mass M, or a pressure p, suddenly changes. We suspected that the action is not able to handle such a situation at all. There is no solution for the Einstein field equations then.
Cylinders with a shear
Now we can analyze our cylinder with a shear examples. If the Einstein-Hilbert action would treat a positive R as positive potential energy, then we could try to find the minimum energy state for the cylinder. There probably exists one.
But since a positive R is "kinetic" energy or "positive potential energy", such a procedure is not possible. The action may simply fail to have a stationary point at all.
Looking for a stationary point of the Einstein-Hilbert action S, starting from a wrong metric g
Let us have a spherically symmetric uniform mass M of a density ρ. The interior and exterior Schwarzschild solution is a "stationary" point of S. A variation δg of the metric does not change the value of S. Let the metric be g.
What happens if we suddenly and magically, increase the mass M and the mass density ρ:
M' > M, ρ' > ρ ?
We try to find a stationary point of S by applying finite variations δg to the metric g.
A finite variation can never transform g into the new solution of the Einstein equations, g'.
How does the optimization of g proceed? Toward a singularity?
negative
R
|
v r₀
------__ __-----
\_ _/
••• positive R
Let us consider the following very simple model where we adjust the metric g --> g' at short radial distances to match the Schwarzschild metric of M'. But we cannot adjust the infinite space to M'. The metric far away is stuck to M < M'.
The transition between the two metrics is at r₀, where the Ricci scalar R is negative.
The variation δg. At
r < r₀,
we increase g₀₀ --> g₀₀' upward (≈ -1), and g₁₁ --> g₁₁' upward (≈ 1). The Ricci curvatures there are
R₀₀ ≈ 1/2 κ ρ,
R₁₁ ≈ 1/2 κ ρ.
The Wikipedia formula
says that the variation δg decreases the integral of R. The negative R around the transition radius r₀ wins over the positive R that we add inside the mass M'.
... (to be continued).
Manipulating the distance between two masses
-->
● ●
m m
Let us assume that g is the metric for two masses m, given by the Einstein field equations. Let us now change the coordinates in such a way that the geometry of spacetime stays as is, but the coordinate lines move a little bit and transport the masses closer to each other.
What happens to the action S? The R part stays as is, but the LM part changes. We found a small variation of the metric, such that it does not keep S constant?
How can the variation of the action S work at all if we always can find a variation which changes the value of S?
Is it so that the variation is always assumed to be a simple variation which only stretches locally some components of g, and does not contract them in the same variation?
Can we somehow ban "bad" variations? Or define the kinetic energy of a particle in such a way that a bad variation is not able to change the value of LM?
Defining the velocity of a particle in general relativity
Literature is silent about how we define the velocity of a particle P in general relativity. An obvious choice is to take the coordinate velocity of P and convert it with the metric g to a proper velocity.
Definition of the velocity of a particle. We have an observer sitting static at certain spatial coordinates x, y, z. The observer measures the proper velocity of the particle.
A "rogue" variation δg which changes the value of the Einstein-Hilbert action S
^ move
| P (x, y, z)
• •
• • • •
• • • • particles
• • metric g
Let us have particles initially static in a uniform spherical constellation. Let the metric be g from the Einstein field equations.
Let P be a particle at the edge of the sphere, at coordinates (t, x, y, z).
Let us apply an infinitesimal metric variation δg which keeps the spacetime geometry as constant, but "moves" the coordinate location (x, y, z) away from the sphere. Then the mass of P goes to a higher gravity potential, that is, in the action integral S, the volume element sqrt(-det(g)) has a larger value when we integrate over the mass m of the particle P.
The action integral of the Ricci scalar R does not change at all, because the spacetime geometry does not change in any way. But the integral of LM becomes smaller, because the "potential energy" of m is now larger. The lagrangian LM is of the form:
kinetic energy - potential energy.
Thus, the infinitesimal variation δg changes the value of the action integral S, even though we had a solution g of the Einstein equations, and S should not change.
A lagrangian of newtonian mechanics should prevent such a movement of a particle P by having the kinetic energy of P change in the movement.
Could we define "canonical coordinates", which are fixed to the spacetime metric. Then the rogue particle would have a positive kinetic energy relative to standard coordinates, which would restore the value of LM to its original value?
However, e.g., in an expanding universe, it is a hopeless task to define such canonical coordinates.
If the spherical constellation of particles above is held static with pressure, then the potential energy of the particle P does not change if it is moved infinitesimally. This is because the gravity force and the pressure force are in an equilibrium. This may explain why the Schwarzschild interior solution is reasonable.
Analyzing the pressure change in a spherical mass
Our November 5, 2023 counterexample to the Einstein equations involves a changing pressure inside a sphere which is not in a static equilibrium.
^
<--|--> metric g
v
positive pressure p inside
\_____________________________/
----> negative pressure -P <----
in surface
Let us start from a spherical vessel where a negative pressure in the surface compensates a positive pressure inside. We assume that the metric g is a solution of the Einstein field equations.
What happens if we suddenly (or slowly) remove the negative pressure -P from the surface of the vessel?
Is it possible to evolve the metric g in such a way that the change of R still balances a radically changed LM?
Our November 5, 2023 analysis suggested that the metric outside the vessel should be changed, in order to adapt the metric to the sudden lack of a negative pressure. But we cannot change the external metric with a variation which is in a finite spatial volume. At the edge of such a variation there will be an area which has the Ricci scalar R ≠ 0. That is not allowed because the edge is in empty space.
On the other hand, if we allow variations of the metric throughout space, then the Einstein-Hilbert action does not work at all, as we showed on May 10, 2024. Such variations would also break the speed of light, and lead to all the problems with superluminal communication.
Conclusions
Let us close this blog post.
We have to figure out if there is a way to ban "rogue" variations of the metric. The Einstein-Hilbert action S does change in a bad variation, even if the metric g would be a solution of the Einstein field equations.
If a system is static and in an equilibrium, then LM does not change if particles move an infinitesimal distance. In that case, also "rogue" variations are benign.
We have to analyze further, why the Einstein field equations do not have solutions for cylinders with a shear (if we calculated right in March 2024). We have to check the correctness of the 1939 paper by Oppenheimer and Snyder.

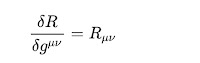

No comments:
Post a Comment