This is a surprising result because one would guess that the acceleration is linear in perturbations.
The metric of a mass flow
Let us determine the metric of the mass flow which we introduced in the previous blog post.
1 3
\ / ^
\ / / v
\__________/
2
^ V
|
• m
We sum the metric perturbations for each part of the mass flow. We are interested in the metric close to the test mass m. The parts 1 and 3 point directly at m.
Let us first determine the metric perturbation which is caused by the part 1 of the mass flow.
r' = distance (M', m)
M'
-------•----------- • m
R₂ R₁
ρ = mass / length
mass flow
------> x
Let us temporarily choose the part 1 as the x axis. Then it is easy to calculate the perturbation at m, which is also located on the x axis. Let the moving frame be comoving with the part 1. Let us have ρ dr as a mass element of the flow 1.
Then the line element for the metric around ρ dr is:
ds² = (-1 + rₛ / r') dt'²
+ (1 + rₛ / r') dr'²
+ (r' dφ')².
We write
dr' = dx',
r' dφ' = dy',
because the contribution to dr' from dy' close to m is essentially zero. Then
ds² = (-1 + rₛ / r') dt'²
+ (1 + rₛ / r') dx'²
+ dy'².
The Lorentz transformation gives:
dt' = γ dt - γ v / c² * dx,
dx' = γ dx - γ v * dt,
dy' = dy.
Let us set c = 1 to simplify the calculations. The metric in the laboratory frame is
ds² = γ² (-1 + rₛ / (γ r))
* (dt² - 2 v dt dx + v² dx²)
+ γ² (1 + rₛ / (γ r))
* (dx² - 2 v dt dx + v² dt²)
+ dy²
= γ² (-1 + rₛ / (γ r) + v²) dt²
+ γ² (1 + rₛ / (γ r) - v²) dx²
- 2 γ v rₛ / r * dt dx
- 2 γ v rₛ / r * dx dt
+ dy².
Note that the metric is at one moment of the laboratory coordinate time t. Since the part ρ dr is moving at a velocity v, the metric is time-dependent.
We dropped the terms ~ v² rₛ, because we assume that rₛ << v << 1. The metric is almost orthogonal since v rₛ is very small.
To obtain the metric near m, we need to integrate over the radii R₁ + x to R₂ + x, where x is the displacement from the test mass m on the x axis. That is, we set x = 0 at m.
However, in the geodesic equation we are interested in the derivatives of the metric g. It is better to calculate the derivatives directly.
The perturbations of individual parts ρ dr are time-dependent. But the sum of all the perturbations is time-independent. The time derivatives of the integrated metric are zero. It is enough to calculate the derivatives with respect to x and y.
We have:
dgₜₜ / dx = dgₓₓ / dx
R₂ + x
= 2 γ ∫ G ρ / r² * dr
R₁ + x
= 2 γ G ρ
* (1 / (R₂ + x) - 1 / (R₁ + x))
= 2 A(x),
where A(x) is the newtonian gravity acceleration caused by the mass in the part 1.
We have
dgₜₓ / dx = dgₓₜ / dx
= -4 v A(x).
The acceleration from the geodesic equation
1
\
\ \ v
\ v
β
\ ^ V
\ |
• m
\
y v a
__--->
\
\
v x
Using the coordinates of the previous section, the velocity of m is
Vₓ = -V cos(β),
Vy = V sin(β).
We are interested in the acceleration of m to the x and y directions. The y acceleration relative to the proper time τ of the test mass m is
d²y / dτ² = 0,
that is, the y velocity Vy slows down as the proper time of m slows down. The Christoffel symbols relevant for the x acceleration are:
Γₓₓₓ = A(x),
Γₓₜₜ = -A(x),
Γₓₜₓ = 4 v A(x) - 4 v A(x) = 0,
Γₓₜₜ = 4 v A(x) - 4 v A(x) = 0.
The acceleration is
d²x / dτ² = 1 / gₓₓ(x)
* ( A(x) * (dx / dτ)²
+ A(x) * (dt / dτ)² )
<=>
d²x / dt² = 1 / gₓₓ(x)
* ( -A(x) V_x² + A(x) ).
The accelerations do not depend on the sign of v. If we calculate the accelerations due to the part 3 of the mass flow, they are symmetric relative to the the part 1. This means that the parts 1 and 3 do not cause any horizontal acceleration.
The part 2 does cause acceleration to the right.
If we calculate the accelerations using the private interaction model, the result agrees for the part 2, but does not agree for the parts 1 and 3. In the private model those parts cause acceleration to the right.
The accelerations of the mass flow in the turns of the flow between 1 and 2, and 2 and 3, contribute a net acceleration straight up.
Thus, the private interaction model gives a different result from the metric.
How can a metric perturbation be "nonlinear" in such a way that the sum gives a different acceleration from the sum of individual accelerations?
1
\
\
\________ 2
---> v
^ V
|
• m
The reason is that the metric does not understand what happens when a mass element ρ dr turns from the part 1 to the part 2. Thus it is the acceleration of the mass elements, after all, which spoils the calculation with the summed metric perturbation.
The acceleration of m is due to it diving deeper into the gravity field of the moving mass elements ρ dr in the part 1 of the mass flow. But when an element comes to the turn between 1 and 2, the element suddenly "disappears" from the integral. The potential of that element vanishes and m magically jumps up into a higher potential.
Can we somehow fix the metric so that it would not be confused by this case?
The "private interaction" model does handle this.
The metric should be augmented with a mechanism which tells us what happens to the test mass m when a mass element is accelerated.
A partial solution: calculate the metric letting the parts of M "fly loose"?
Since the metric cannot handle an acceleration of a mass element of M, let us remove all the accelerations for a short moment. All the parts of M fly freely and there is no acceleration in their path. Then we can calculate the sum of the metric perturbations.
Though this will not work if the acceleration of the mass elements happens to impose an "important" acceleration just at that moment.
Also, the solution only works for a short moment, as the free-flying parts of M soon are dispersed and do not describe the true state of M any more.
In the case of a rotating disk, letting the parts "fly loose" makes the configuration and the metric time-dependent. It is not a beautiful solution.
Conclusions
We were able to solve the mystery of why the calculations on August 10 and August 29, 2023 gave different values for the frame dragging by a rotating disk. Our August 10 calculation claimed that the gravitomagnetic moment is 1/2 J, while the August 29 calculation said that there is no frame dragging at all. The reason is that the concept of a "metric" does not understand a configuration where parts of the mass M are under an acceleration.
The value for the gravitomagnetic moment of a rotating disk is 2 J in the literature. We believe that value is incorrect.
It is not clear if we can mend the concept of a metric to handle mass elements which are under an acceleration. If not, then the "private interaction" model, which we have introduced, is the correct way to describe a many body system where the parts are accelerating.

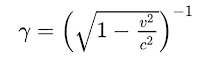


No comments:
Post a Comment