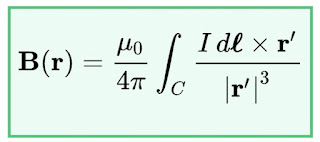UPDATE December 9, 2023: We still have problems with the "inertia force". If in a radial motion, we need to have the extra inertia 2 U, but the inertia force is defined as it would only be U. The calculations below are erroneous. We will write a new blog post in December 2023.
----
UPDATE November 27, 2023: We formulated a new inertia rule for an electric field where any interaction increases the inertia of q. See our November 26 blog post.
----
UPDATE November 24, 2023: We probably have to assume that the potential U between two negative charges dq and q increases the inertia of q, (and decreases, if dq is positive). This makes more sense than our previous claim that the repulsion between dq and q paradoxically reduces the inertia of q. That claim leads to a nonsensical result that an electron in a potential less than 511 kV would have negative inertia.
We also have to assume a "paradoxical momentum exchange" between dq and q.
----
In our September 23, 2023 blog post we asked if a mass flow coming directly toward a test mass m exerts a specific force on m, besides the usual gravity force.
^ v
/
● dm ● dm
\
v v
• m
If we have an individual mass dm approaching m, or receding from m, then the Schwarzschild solution says that the extra inertia of m in the field of both dm's in the diagram pushes m to the right in the diagram. An open question is what happens if there is a constant mass flow. The gravity field stays constant, though the individual mass elements change. Why should the inertia inside the field push m to some direction?
We have the exact same question about the electric field. In the case of the electric field, we may have empirical data which resolves the question. Let us check if the standard formulae for calculating the magnetic field of a coil include the effect from the inertia inside the electric field of a charge approaching a test charge directly.
Definition. An interaction is private if a flow of charge Q moving directly toward a test charge q causes an inertia effect on q that can be summed from the inertia effects of elementary charges dq in Q.
On September 4, 2023 we derived the magnetic field of a straight electric wire, using the Schwarzschild metric. We used the "privacy" assumption there. It contributed 2/3 of the acceleration to the direction of the wire. Let us check our calculations again.
The Biot-Savart law
The Biot-Savart law gives a zero magnetic field in the direction of a wire element dl, because of the factor dl × r'.
The magnetic force should depend on a non-zero velocity V of a test charge q in the laboratory frame. If q is static, and the extra inertia inside the field of Q pushes q, that is another kind of a force.
Changes in the inertia of a charge inside an electric field: assumptions
We assume that dq and q both have a negative charge. We use the hypothesis of our September 4, 2023 blog post, but with the sign flipped:
Conjecture about inertia inside an electric field. If q and dq have the same sign, then the inertia of q relative to dq in a tangential motion, inside the electric field of dq, is increased by the potential energy
U = 1 / c² * 1 / (4 π ε₀) * |q| |dq| / r²,
where r is the distance between q and dq. In a radial motion the inertia increase is double of that: 2 U.
If q and dq have different signs, then the inertia decreases by U.
Assumption about the "inertia force". The inertia U "has the velocity of" dq when q acquires it. In a radial motion, only a half of the extra inertia 2 U has the velocity of dq.
Assumption about paradoxical momentum exchange. When q gains more inertia in the electric field of dq, and the charges of q and dq have the same sign, that paradoxically speeds up the velocity of q relative to dq. The sign of the inertia force is flipped.
The paradoxical assumption is required to get the sign right in the magnetic force. The assumption really is paradoxical because if dq and q have the same sign, and q approaches dq, we would expect the extra inertia of q to slow down the movement of q relative to dq.
We use the paradoxical assumption to derive the magnetic force, which never speeds up the velocity of q. Thus, we do not need to face the problem from where q would acquire the energy for the speedup in its velocity. The paradoxical assumption might be associated with the hypothesis that positrons are electrons moving backward in time. We have to investigate that.
If the electrons do not move, then there should be no change in inertia. That happens because the changes in the inertia of q due to dq and -dq cancel each other out.
But why should we take into account the inertia when the electrons move in the wire? Is the inertia "private" to each dq, and if a dq moves, then we have to take into account the effects of the movement? The inertia is "attached" to a certain dq.
But if the inertia is "private", why there is no extra inertia from the energy flow between the fields of different dq and -dq? That energy flow would double the inertia change in a radial movement. We have used the energy flow argument to explain extra inertia in a gravity field.
The acceleration imposed by a wire element, using our own conjecture about the inertia inside an electric field
dl \
\ v = electron velocity
v ρ = electron charge per length
r = vector (dl, q)
r = distance (dl, q)
^ V
|
• q
^ y m
|
------> x
Let us determine the acceleration of q in the general case where dl is a wire element. We have protons and electrons in the wire element dl. We will determine the acceleration of q by switching to the comoving frame of the electrons, calculating the acceleration of q there, and Lorentz transforming the acceleration to the laboratory frame.
dl
\ dq = electrons
\
\ -dq = protons
\ v
v
We assume that
|v| << |V| << c.
We can ignore ~ v² terms and ~ |v| V² terms. The relevant terms are ~ |v| |V|.
The wire element dl contains protons worth a charge -dq, and electrons worth dq. The electrons move along the wire at a velocity v.
In the comoving frame of electrons in the wire.
In the comoving frame of dq, the factor
γ = 1 / sqrt(1 - v² / c²)
≅ 1 + 1/2 v² / c².
The terms which come from the correction 1/2 v² / c² are ~ v² and can be ignored because we assumed that |v| is small. We can pretend that γ = 1.
Definition. Let us define the effective inertial mass M of q under a force F through the formula
M = |F| / |a|.
Note that the force F and the acceleration a may have slightly different directions, because of special relativity. The definition assumes no fields interacting with M. They can alter the inertia.
The effective inertial mass M depends on the relative direction of F and the velocity of q, and the absolute value of the velocity. Generally, the effective inertial mass for a slow velocity V is of a form
M(F, V) = m + C(δ) m V² / c²,
where
1/2 ≤ C(δ) ≤ 3/2,
and C depends on the angle δ between F and V. We have C = 1/2 if F and V are normal and C = 3/2 if F and V are parallel or antiparallel.
1. The Coulomb force Fc on q, due to the electric repulsion between dq and q in the comoving frame, is
Fc = 1 / (4 π ε₀) * q dq / r² * r / r,
where r is the vector from dq to q, and r is the length of the vector. We assume that dq and q are both negative charges.
What is the acceleration that Fc causes on q inside the field of dq?
Let Vr be the radial velocity of q relative to dq, and Vt the tangential velocity. The momentum of q is approximately
p = (m + 1/2 m Vr² / c² + 1/2 m Vt² / c²)
* (Vr, Vt),
where U is the potential energy of the repulsion between dq and q.
The Coulomb force changes the radial velocity and the radial momentum of q.
The derivative of the radial momentum with respect to Vr is
M = m + 1/2 m Vt² / c² + 3/2 m Vr² / c².
That is the "radial inertial mass" of q if we do not include the interaction.
Let Fc push q some distance farther away from dq. Then q gains radial kinetic energy worth some W, and its radial inertial mass would grow by 3 W / c², but since q loses inertia worth 2 W / c², the net gain of inertial mass is W / c². We can pretend that the inertial mass of q is in a radial motion:
M = m + 1/2 m V² / c².
2. The inertia of q increases when it dives deeper into the electric field of dq. The test charge q acquires from dq extra inertia which "moves along with dq".
This causes an additional "inertia force" Fi based on the velocity of q:
Fi = -dW / dt * 1 / (M' c²) * (V - v)
= -1 / (4 π ε₀) * q dq / r²
* (V - v) • r / r
* 1 / c² * (V - v)
= -Fc • (V - v) / c² * (V - v)
= -V (Fc • (V - v) / c²) + v (Fc • V / c²).
Above we use the paradoxical assumption. Otherwise, q would be accelerated to the opposite direction.
We will calculate below that the magnetic field of the wire does not actually change the absolute velocity of q. The above assumption is a hypothesis which makes the mathematics to work, but does not result in any actual speedup.
Switch back to the laboratory frame.
We have to apply the Wikipedia formulae posted above to convert the accelerations to the laboratory frame. We can ignore ~ v² terms.
To obtain the accelerations due to forces, we have to divide by the effective inertial mass M(F, V). A problem is that the angle of F relative to V - v is slightly different from the angle relative to V.
Let us divide the force Fc into the component Fn which is normal to V, and to the (anti)parallel component Fp.
Without the interaction, the inertial mass of q to the direction of V - v is
m + 3/2 m (V - v)² / c².
What is its inertial mass to the slightly different direction V? The value of C above is a well-behaved function of the angle between the force and the velocity of q, and the velocity itself. The angle is at most ~|v| / |V|. From the Taylor series for C, we get the result that the inertial mass to the direction of V is
m + (3/2 - C' v²) m (V - v)² / c²,
where C' is essentially a constant for small |v|.
From the Lorentz transformation of an acceleration, we obtain the approximate acceleration due to Fc:
ac = (Fc (1 - 2 v • (V - v) / c²)
- Fc • v (V - v) / c²)
/ (m + (1/2 - C' v²) m (V - v)² / c²)
= (Fc (1 - 2 v • V / c²) - V (Fc • v / c²))
/ (m + 1/2 m V² / c² - m V • v / c²)
= (Fc (1 - 2 v • V / c²) - V (Fc • v / c²))
/ ((m + 1/2 m V² / c²) * (1 - V • v / c²))
= (Fc (1 - v • V / c²) - V (Fc • v / c²))
/ (m + 1/2 m V² / c²).
The first term "1" above is canceled by the corresponding acceleration caused by the protons, -dq, in the wire segment dl. The third term is canceled by the second term in the inertia force:
ai = (-V (Fc • V / c²) + V (Fc • v / c²)
+ v (Fc • V / c²))
/ (m + 1/2 m V² / c²).
The first term above is canceled by the corresponding inertia force by the protons. The second term is canceled by the third term in ac. We get:
ai + ac = v (Fc • V / c²)) / (m + 1/2 m V² / c²)
- Fc (v • V / c²) / (m + 1/2 m V² / c²).
The Biot-Savart law says that the acceleration should be
abs = q / m * V × 1 / (4 π ε₀) * 1 / c² * 1 / r²
* dl ρ v × r / r
= 1 / c² * V × v × Fc / m
= v (Fc • V / c²) / m
- Fc (v • V / c²) / m.
Since V² is very small, it is essentially the same result which we obtained above.
Biot-Savart contradicts the laws of other conventional electromagnetism
Let us have arbitrary moving charges in a system, and a test charge. We can handle each individual charge by switching to its comoving frame and using Coulomb's law. Then switch back to the laboratory frame.
In this way we should obtain the complete electromagnetism, with the magnetic field included. But we know that it is not possible to derive electromagnetism solely from Coulomb's law and special relativity. Thus, conventional electromagnetism contradicts special relativity. Apparently, it is not Lorentz covariant.
Conclusions
Using our hypothesis about the inertia of a test charge, we were able to derive a formula which agrees with Biot-Savart.
We also proved that conventional electromagnetism plus special relativity clash with Biot-Savart and other rules about magnetism. This shows that conventional electromagnetism is self-contradictory. We can expect slight corrections into its rules.
Our calculations about the inertia above ignored the effect of the accelerating movement of the electrons in a wire which is not straight. The drift velocity of electrons in a typical wire is very slow, only a few micrometers per second. The effect of frame dragging or the acceleration of the electrons may be quite small.
Our model explains the orbit of a test charge q close to a wire containing a current. But the model does not describe the (significant) energy and momentum stored in the magnetic field. The Maxwell equations describe the energy and the momentum, at least partially. Classical electromagnetism is silent about the self-force which the Coulomb field of a charge imposes on the charge itself. In our blog we have earlier taken the first steps to model the self-force. Recall our rubber band models of the Coulomb field.