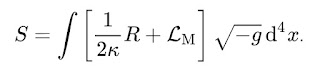The Minkowski & newtonian model predicts dark energy

According to literature, observations are consistent with the hypothesis that the velocity of cosmic expansion has been constant since the Big bang.

https://en.wikipedia.org/wiki/Expansion_of_the_universe

That is, if we put ourselves at the origin of the spatial coordinates, a typical baryon B has been receding from us at a constant velocity v for the past ~ 14 billion years.

Let us check. The Hubble constant is either 73 km/s/Mpc (standard candles) or 68 km/s/Mpc (CMB). The two different estimation methods give conflicting values.

A megaparsec is 3.09 * 10²² meters.

       t₁ = 1 megaparsec / (73 km/s)

           = 13.4 billion years,

       t₂ = 1 megaparsec / (68 km/s)

           = 14.4 billion years.

The values agree with the current estimate

       t   = 13.8 billion years.

Observation of the inertia of small shells of mass implies that something must cancel the extra inertia in a linear movement

In the previous blog post we argued that the inertia of the masses in a small expanding and contracting shell (= radial movement) should be smaller than in a linear movement if the system is deep in the potential well caused by neighboring masses.

The masses in the observable universe might make the inertia of a linear movement 10% larger than for a radial movement.

We do not know how precisely people have measured the inertia in various synchronous movements, but the difference has to be much less than 10%. Someone would have noticed it, if the difference would be that large.

Our conclusion is that negative energy or negative pressure must almost exactly cancel the inertia which would be caused by the mass of distant galaxies. There is a problem of fine-tuning in this.

Or, the maximum range of gravity is of the order 200 million light-years. Then there is no fine-tuning, but it does not look nice to assume an arbitrary maximum range.

A negative cosmological constant

https://en.wikipedia.org/wiki/Friedmann_equations

In the standard ΛCDM model of the universe, dark energy is the cosmological constant Λ.

In the above equations k = 0 if the spatial metric is flat. Observations suggest that it is flat. The Hubble constant is H and a is the scale factor.

For H to stay approximately constant, a negative value of Λ must contribute considerably to the mass-energy density ρ. A negative Λ produces negative pressure.

A dust ball explosion in the Minkowski space

The spatial metric of a uniform expanding dust ball probably is flat if the particles will reach the infinity and their velocity is zero there. Here we assume that gravity is the only interaction.

1. A negative cosmological constant would correspond to an ad hoc scalar field which has positive energy density and which for an unknown reason expands with the dust ball. This hypothesis is ugly.

2. Suppose that there are particles which repel ordinary matter. The particles are dark matter and are spread quite evenly inside the dust ball. Their repulsion could be fine-tuned to cancel the gravity of distant parts of the dust ball. The repulsion cannot be between ordinary matter particles, because then we would have no gravity and no stars.

A possible way to fine-tune: we demand that the sum of the "gravity charges" of all particles in the universe must be zero. This would be analogous to the fact that electric charges seem to cancel each other out in the universe.

The spatial metric of comoving coordinates would be hyperbolical. The large-scale geometry for static observers would be Minkowski. The velocity of the expansion stays constant.

3. If the maximum range of gravity is ~ 200 million light-years, it would keep clusters of galaxies together, but allow the universe at a large scale to expand at a constant velocity. The spatial metric at a large scale would be hyperbolical, since that is the geometry of comoving coordinates for an explosion with no gravity in the Minkowski space. The ad hoc parameter 200 million light-years is ugly.

Of these alternatives, 2 looks the least ugly.

Negative gravity charge particles

If the universe is teeming with dark matter particles with negative gravity charges, why we have not noticed them? Maybe negative gravity charge particles do not clump together, but stay free.

Negative gravity charge particles can not be used to create negative gravity in the sense that they would reduce the inertia of an ordinary particle and make clocks to tick faster. All interactions add to the inertia of a particle. It does not matter if the interaction is repulsive or attractive.

The inertia of a negative gravity charge particle is positive. It is just like an ordinary particle, but repels all particles of ordinary matter.

The kinetic energy of a negative gravity charge particle would add its negative gravity charge, just like kinetic energy adds to the mass-energy of an ordinary particle.

A negative gravity charge particle does not annihilate easily since it repels positive gravity particles.

Negative gravity charge particles are another step in reducing gravity to just an ordinary force.

Conclusions

We need a mechanism which explains why distant galaxies do not considerably increase the inertia of a linear motion.

It turns out that the same mechanism causes the universe to expand surprisingly fast - the mechanism is equivalent to dark energy.

We still have the mystery of why the ordinary matter and dark matter densities of the universe are relatively close to the density which makes the spatial metric flat. The matter content is estimated to be 30% of what is required for a flat metric. In ΛCDM the equivalent problem is why the universe entered the "dark energy dominated" period quite recently.

The inertia of charges moving inside a spherical shell of charge: implications for cosmology

We have to analyze in more detail the energy flow in an electric field where charges move.

Electrons inside a positively charged sphere

Suppose that we have a positively charged spherical shell, and electrons move inside it.

                       +     +     +

                  +                      +

                +                          +

                +                          +

                  +                      +

                       +     +     +

If we have just a single electron, it is carrying its negative potential energy around, and its inertia has grown by the absolute value of the potential energy.

But what if we have a whole cloud of electrons randomly bouncing around?

The electric field of the system does not change much when the electrons bounce. Has the extra inertia gone away?

That does not sound right.

What if we have a little shell of electrons inside the shell of positive charge? The shell keeps expanding and contracting. The outside field of the shell does not change appreciably. Is the inertia of the electrons in the shell still the same as for random electrons bouncing around?

The Poynting vector does not show any energy flow in this case. The logical conclusion is that the electrons in the little shell do not have extra inertia in that kind of a coordinated movement.

If the inertia of the shell turns out to be the same as for random electrons, then the field of each electron has to be "private", so that Nature can track the energy flow separately for each individual electron. That would be surprising.

Implications for gravity and cosmology

There are no reports that the inertia of masses of a shell in a radial movement would be less than the inertia in other kinds of a movement.

Either our reasoning above does not hold for gravity, or the effect of distant masses on the inertia is very small.

The effect should be of the same order of magnitude as other general relativistic effects. On the surface of Earth the effect of Earth's gravity is ~ 10⁻⁹.

The effect of the gravity of the Milky Way is ~ 2 * 10⁻⁶.

The effect of the gravity of the local cluster of galaxies is ~ 10⁻⁵.

https://en.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_experiment

The equivalence of the inertial mass and the gravity mass has been measured to an accuracy 10⁻¹⁵. We have to check if the experiments would have noticed a difference in coordinated movements of masses.

Measurements of the gravity constant G keep giving conflicting results

https://en.wikipedia.org/wiki/Gravitational_constant

The variation in measurements of G is a whopping ±0.03%, and the uncertainty has not been reduced in the past 80 years.

A possible reason for the discrepancies in the measured values is that the inertia of the torsion balance depends on the way that the masses in it move.

We have to check the design of the balances which researchers have used.

What is the speed of light outside the observable universe?

If the observable universe is embedded in the Minkowski space, and if the matter in the observable universe creates a potential well, then the speed of light in the observable universe is slower than in the surrounding, possibly empty, Minkowski space.

Then the speed of light which we observe would not be the largest possible speed of a signal.

Question. What is the gravity field of an explosion like? If the fringes of the explosion are receding from us faster than the local speed of light, are we in a potential well or not?

Inertia caused by an expanding sphere of electric charges - retardation

                       +     +     +

                  +                      +

                +                          +

                +       e-  ● --->    +

                  +                      +

                       +     +     +

Suppose that we move an electron inside a static spherical shell of positive charges. The magnetic field generated by the moving electron will make the Poynting vector non-zero outside the sphere. The Poynting vector describes energy flow in the field. The energy flow explains the extra inertia which the electron feels.

However, the magnetic field of the moving electron does not immediately reach the electric field outside the sphere. There is a delay which is caused by the finite speed of light.

How does Nature know beforehand that there will be energy flow, and the electron should feel extra inertia?

The problem sounds very much like the problem of how Nature makes sure that momentum and energy are conserved in all processes, despite delays caused by the finite speed of light.

In retardation of the electric field, Nature seems to calculate beforehand where a charge will be.

Suppose then that the sphere of positive charges is expanding fast. When the magnetic field of the moving electron reaches outside the sphere, the sphere has expanded greatly. The Poynting vector will generate much less energy flow than for a static sphere. The inertia is equivalent to the case where a static sphere is very large.

In gravity, this means that inside a rapidly expanding explosion cloud the inertia which masses feel is much less than for a similar static cloud. Clocks tick much faster than in a static cloud.

Conversely, inside a rapidly contracting ball of dust, masses feel surprisingly much inertia, and clocks tick surprisingly slowly.

The depth of a potential well can be defined by the redshift of light sent from the well to faraway space. The redshift is determined by how much slower clocks tick inside the well. We see that the potential well inside a rapidly expanding explosion cloud is surprisingly shallow.

Suppose that we have a rapidly moving large charge Q passing a test charge q. The behavior of q is calculated by switching to a frame where Q is static. In that frame we can assume that Q has a static electric field which has a potential function. In the new frame Q may be very far from q when we move q to determine the inertia of q, even though in the old frame Q was close.

Dark energy cancels the inertia that would be caused by the masses in the observable universe?

The inertia caused by the local cluster of galaxies should be ~ 10⁻⁵. The inertia grows by

         r³ / r

as we add the effect of the mass within the radius r from us. This is because the total mass grows as r³ and the gravity potential at the edge of the mass declines as 1 / r.

Thus, the masses of the observable universe might contribute 10% more inertia for a test mass in a linear movement.

There certainly is not 10% more inertia in a linear motion than if we construct a small expanding and contracting shell of mass on Earth.

A possible explanation is that dark energy balances the effect of mass and cancels the extra inertia for a linearly moving mass.

A possible alternative solution: the total energy of the explosion is zero. The final state is infinitely redshifted radiation spreading into the Minkowski space. We have to study the zero energy hypothesis of the universe. The extra inertia from the large-scale structure would be zero.

If the total energy of the universe is zero, then large-scale gravity in the universe is zero. The spatial metric is the flat Minkowski metric. Clocks tick at the same rate as in the surrounding Minkowski space.

A zero energy universe would have a constant expansion rate. We have to check if the measurements about the expansion rate are consistent with a constant expansion rate.

The recursive growth of inertia close to an event horizon

We have barely touched the question why the speed of light drops to almost zero at a Schwarzschild black hole horizon. The inertia of a test mass m shoots up toward infinite.

The negative potential of a test mass m at the horizon is

       -m c²,

which can only explain a doubling of the inertia.

Recursive inertia

Let us have static observers who form a sequence toward the horizon.

The potential of a test mass m at the nth observer is

       (0.99ⁿ - 1)  *  m c²,

and the "remaining energy" of the test mass m is

       0.99ⁿ  *  m c².

The remaining energy is the energy which a distant observer would receive if we would convert the test mass to photons and send them to the distant observer.

             observer n        ●

 

             observer n + 1  ●    •  test mass m

                                                1% less mass-energy

                                                1% more inertia

           ------------------------------------- horizon

     

If the observer n + 1 is holding the test mass m, then the observer n thinks in his local frame that the mass-energy of the test mass is 1% less than if the observer n himself would be holding it.

Since the test mass carries along that 1% of negative potential energy, the observer n thinks that the inertia of the test mass in a horizontal movement is 1% larger than when the observer n himself is holding it.

The inertia is easiest to understand for observers 0 and 1. The observer 0 is far away in space, and the test mass close to him has the inertia m.

If the observer 0 lowers down the test mass to the observer 1, then the test mass will carry along negative potential energy -0.01 m. The inertia in a horizontal movement is 1.01 m.

The inertia grows exponentially as we go to ever lower observers:

       m / 0.99ⁿ.

How is the exponential growth possible? The reason must be that the extra inertia itself acquires ever more inertia as we go lower.

The extra inertia comes from energy flow in the newtonian gravity field. The lower we go toward the horizon, the more inertia a certain amount of energy in the field holds.

The inertia in the radial direction is 2% larger for the observer 1 than for the observer 0. We have to find a reason why also the radial inertia grows exponentially:

       m / 0.98ⁿ.

The series of errors which led from Einstein to the black hole information paradox

Let us once more write down the logical sequence of errors, which almost inevitably led to the black hole information paradox, and to development of strange physical models to "solve" a paradox which never existed.

1. Albert Einstein in 1915 thought that gravity determines the "spacetime geometry" and is not just another force.

2. People started to believe that the "spacetime geometry" has infinite forces with which it can make anything to obey its orders. No one calculated the backreaction of the Einstein field equation solutions to a small test mass. We conjecture that the equations do not exert infinite forces on a test mass, if calculated correctly.

3. Since the spacetime geometry is infinitely strong, so is the event horizon of the Schwarzschild solution.

4. An infinitely strong horizon is a one-way membrane.

5. Now we have a problem: a test mass can never reach the horizon. Solve the problem with a mathematically incorrect switch to Eddington-Finkelstein coordinates.

6. A one-way membrane breaks thermodynamics. Jacob Bekenstein and Stephen Hawking realized this.

7. Rather than correcting the errors 1 - 5, Hawking devised a way to pull radiation out of the infinitely strong event horizon.

8. We arrive at the black hole information paradox.

9. Rather than correcting the errors 1 - 5 and 7, people started to develop string "theory", holography, and so on, to solve the non-existent paradox.

The series of errors happened because we cannot make empirical measurements of event horizons. Empirical tests would have cut short the sequence of errors.

The errors in black hole research: a summary of our findings so far

We have made a lot of progress in analyzing various errors in theoretical black hole research done since the year 1960.

Empirical research of black holes is robust

The research which rests on empirical data is robust:

1. We know that black holes do not radiate much in the electromagnetic spectrum. Matter falling in a black hole does not produce the large flash that we would expect if there would exist a surface which it would hit.

2. We know that a binary pulsar radiates away energy at the rate predicted by general relativity.

3. We know that a merger of black holes or neutron stars generates gravitational waves which match the predictions of general relativity.

4. A collapse of a supernova seems to create either a neutron star or a black hole.

Theoretical research of the event horizon and singularities is not robust

1. The metric in the Einstein field equations seems to describe the behavior of a point test mass whose mass-energy is infinitesimal. People failed to calculate the backreaction to a normal particle whose mass is not infinitesimal, and came to believe that the event horizon has an infinite force and is a one-way membrane.

2. A one-way membrane breaks thermodynamics. Stephen Hawking tried to repair the drastic problem by inventing a very unlikely hypothesis about the existence of Hawking radiation. The hypothesis led to an even worse problem of broken unitarity, and the black hole information paradox. Now it was not just thermodynamics broken, but the time symmetry of laws of physics was broken.

3. Rather than question all the dubious steps, many researchers started to believe that Hawking radiation exists.

4. Suggested models to solve the black hole information paradox are very strange. There are ideas of teleportation, wormholes, the same history happening twice, holography, and so on.

5. The notion of the "geometry of spacetime" involves many problems, which are readily visible from the Einstein-Hilbert action. We have analyzed the problems in several blog posts in the past four months. As far as we know, there has been little research on these fundamental problems in the past six decades.

6. The switch from Schwarzschild coordinates to Eddington-Finkelstein coordinates, which eliminates a claimed "coordinate singularity", is mathematically incorrect, unless one accepts that a model of physics can calculate something which happens "after" an infinite time.

7. The supposed collapse of matter into a point singularity would happen "after" the infinite time has passed. Does that make sense?

8. Extending geometries and coordinate systems to include a white hole is extremely speculative.

9. The Schwarzschild metric inside the event horizon probably requires that the event horizon is a one-way membrane. Consequently, the inner metric probably does not describe a real black hole. In the Kerr solution there are even closed timelike loops inside the inner event horizon. It is very unlikely that the inner Kerr metric would be correct for a real black hole. 

Science fiction motives in research of gravity

In our blog post on January 22, 2022 we mentioned that some researchers of gravity like to present ideas which would support science fiction stories, even if those ideas seem to break basic, true-and-tested principles of physics.

We raised cyclic causal loops and traveling back in time as examples of ideas which are motivated by science fiction.

Research of gravity seems to have different standards from other branches of science. If someone working in biology would claim that a certain animal can create an infinite force and travel back in time, people would be highly sceptical.

But a gravity researcher can claim that if we make a small mass to rotate, and compress it to a small space, then the mass can exert an infinite force at the horizon, and one can travel back in time inside it. The mass might even open a road to another universe through a white hole.

There is no empirical evidence whatsoever that infinite forces can exist, or that there are white holes. Traveling back in time seems to be logically contradictory, or would require incredible fine-tuning, so that there would be a loop in a complex sequence of events.

The physics that we know does not allow infinite forces, it does not allow traveling back in time, and matter cannot disappear from a closed box.

In gravity research there also exist motives that could be called religious. Hawking radiation is the prime example. People do not like the idea that objects can fall into a black hole and stay there forever. They hope that there is a "rebirth". Matter magically rises up from the black hole, and is free to fly again.

The derivation of Hawking radiation in Hawking's original 1975 paper is extremely speculative. It is based on a claim that the horizon of a black hole is almost infinitely strong, and can in a mysterious way create radiation from nothing. No one has been able to come up with a derivation which would be convincing.

If someone would present an idea like Hawking radiation in electromagnetism, few people would take it seriously. But many gravity researchers and string "theorists" firmly believe that such radiation exists. It exists even though it creates the black hole information paradox and seems to break unitarity. They rather break physics than give up on the idea of a rebirth.

Creation of new universes from black holes is another idea which sounds religious. It would be nice if a new universe were created. It is a rebirth of another kind.

https://en.wikipedia.org/wiki/How_many_angels_can_dance_on_the_head_of_a_pin%3F

Photo by George Hodan

https://www.publicdomainpictures.net/en/view-image.php?image=17799

We currently cannot make empirical measurements of the event horizon. We cannot measure if the horizon radiates. We cannot empirically study what is inside a black hole.

When there are no empirical tests, "hype" may flourish inside a branch of physics. Researchers debate how many angels can dance on the head of a pin, to quote a 17th century joke about medieval scholasticism.

Collapse of a shell of dust or light in general relativity

We observed on January 21, 2022 that the collapse of a spherical shell of negative charge on a central positive charge causes very little energy displacement in the electric field. Therefore, the inertia of the shell does not grow (except by the added kinetic energy), and the shell collapses fast.

Similarly, a spherical shell of light should collapse fast into a black hole. Observers close to the shell see it collapsing faster than light in their local frame.

What does general relativity say about the collapse of a shell of light or very fast massive particles?

How does general relativity treat faster-than-light particles?

If one could move faster than light in the Minkowski space, then we would face the paradoxes of time travel. We do not think such travel is possible.

https://en.wikipedia.org/wiki/Cherenkov_radiation

On the other hand, if the speed of photons is locally low because of some interaction, then there is no paradox if something else moves at the speed of light in vacuum. An example is a block of glass where photons move slowly, but Cherenkov electrons move fast.

How does general relativity treat faster-than-light particles?

That is a tricky question. The stress-energy tensor is the view of a local observer at a static position according to the spatial coordinates. What does he measure as the energy of a faster-than-light particle?

If the observer were in the Minkowski space, he might think that the energy is infinite?

Should we use comoving coordinates, so that the particle does frame-dragging and does not move faster than light in those coordinates? This would be like the Alcubierre drive.

Maybe particles cannot move faster than light in general relativity?

A collapse of a shell consisting of a single layer of particles

Let us have a shell of dust collapsing in newtonian gravity. We assume that there is no mass inside the shell. The shell probably becomes thinner and thinner because the innermost particles do not feel any pull of gravity.

Let us assume that there is only a single layer of particles. Gravity squeezes the particles in the radial direction. If they are point particles, this is no problem.

https://en.wikipedia.org/wiki/Schwarzschild_metric

Outside the shell we have the Schwarzschild metric

Let r be the radial coordinate of the shell. The radial coordinate speed of light is

       (1  -  r_s / r) * c

where c is the value far away. Clocks tick slowly, and radial distances have grown. That is why the radial coordinate speed of light is slow.

Inside the shell we have the flat Minkowski metric. Clocks run slowly down there, but the spatial metric is the coordinate metric. The radial coordinate speed of light is

       sqrt(1  -  r_s / r) * c.

The speed of light is faster inside the shell.

Now we face a dilemma: if the particles of the shell are moving almost at the speed of light, then an observer, who is static outside the shell, will think that their energy is several times m c², where m is the mass of the particle. However, an observer inside thinks that the particles move significantly slower than light. Their energy might be just a little over m c².

What does a static observer just at the shell think about the energy?

Which observer is right? Whose stress-energy tensor should we use in general relativity?

Let us imagine that the observers suddenly stop the particles. They can harvest some amount of energy. The observers must agree on the amount. Should we use this value in the stress-energy tensor?

But in general relativity, the stress-energy tensor is a local thing. The tensor cannot be aware of what happens if we stop the entire shell from advancing.

The Oppenheimer-Snyder collapse of a uniform ball of dust

https://journals.aps.org/pr/abstract/10.1103/PhysRev.56.455

The Oppenheimer-Snyder 1939 model is not a collapse of a shell, but it is the best researched model of a collapse.

Let us assume that the dust ball is initially static. A clock at the center of the ball ticks slower than a clock at the surface, and observers can measure this. Thus, it is not the FLRW metric, even though several papers claim it is. In the FLRW metric, observers can verify that their clocks run at the same rate.

Oppenheimer and Snyder believed that they must match the metric inside the collapsing ball to the Schwarzschild metric outside the ball.

Let us look at an infinitesimally thin shell of dust at the surface of the dust ball. If the shell obeys the Schwarzschild metric which is outside the ball, it will never reach the event horizon in the Schwarzschild coordinate time.

This means that the ball of dust never becomes smaller than its Schwarzschild radius.

That does not sound right. We would expect the dust ball to contract much smaller. The hamiltonian or lagrangian of the theory is strange if it can bring a system to a total standstill, though the system is clearly in an unstable state.

We argued in the previous blog post that using Eddington-Finkelstein coordinates to jump over the infinity of Schwarzschild time is incorrect physics. New coordinates do not come to the rescue.

A solution to the Oppenheimer-Snyder problem: do not match the metric inside the dust ball to the surrounding Schwarzschild metric

Cherenkov radiation in water in the Reed Research Reactor

https://commons.wikimedia.org/wiki/File:Cerenkov_Effect.jpg#mw-jump-to-license

Consider a block of glass. Light propagates slowly in glass, but Cherenkov electrons can move considerably faster.

Assume that the refractive index of the glass varies from place to place. Observers living inside glass can map the geometry with rays of light, and calculate a metric.

Then Cherenkov electrons arrive, and the observers are perplexed. They see electrons passing them faster than light.

If Cherenkov electrons would be observers, they would think that the block of glass has a very different metric from what glass observers see.

It does not make sense to match the metric of glass observers to Cherenkov observers.

In the case of a collapsing shell, we have claimed that the shell does not acquire extra inertia, and "sees" a metric which is very different from the metric that small point masses see in the Schwarzschild solution. Point masses acquire huge extra inertia close to the horizon.

It may be that there is no sense in matching the metric of a collapsing shell to the Schwarzschild metric.

In our Minkowski & newtonian model the "geometry of spacetime" is something that the fields simulate for small point masses, in certain cases. A collapsing shell sees a different "metric". We should not try to match it to the Schwarzschild metric.

The word "metric" is misleading if we have to calculate the paths of different objects using a toolkit of various rules. When one calculates paths in electromagnetism, one does not use the word metric.

Conclusions

In literature there is debate about the behavior of collapsing shells in general relativity. Do they freeze at the event horizon or not?

The confusion is due to inherent problems in general relativity. It is not clear who should measure the stress energy tensor and how. Neither it is clear how one should match metrics in different zones.

We claim that the basic problem in general relativity is that it assumes the existence of a "metric" which is supposed to describe the behavior of all objects. The phenomena associated with electromagnetism or gravity cannot be reduced to a "metric". Rather, one must calculate energy flow in the fields to determine the inertia of various objects, and proceed from that.

The conversion from Schwarzschild coordinates to Eddington-Finkelstein is dubious

Early researchers of general relativity correctly identified the event horizon of the Schwarzschild metric as a singularity. It is a singularity because keeping a test mass static would require an infinite force. An infinite force cannot arise from a normal hamiltonian or lagrangian.

But later researchers started to claim that the event horizon is just a "coordinate singularity", which is a result from badly chosen coordinates.

https://en.wikipedia.org/wiki/Eddington%E2%80%93Finkelstein_coordinates

A standard procedure to get rid of the "coordinate singularity" is to switch to Eddington-Finkelstein coordinates.

For a test mass falling into the black hole, the Schwarzschild coordinate time goes to infinity before the test mass reaches the horizon.

Eddington-Finkelstein coordinates are based on the tortoise radial coordinate r* which goes to minus infinity at the same rate as the Schwarzschild time coordinate grows to infinity.

One can extend Eddington-Finkelstein coordinates to cover the journey of the test mass through the event horizon and deeper. There is no singularity at the event horizon.

But does the extension make sense?

Extending time past the infinity

Let us imagine that we have an infinite sequence of observers ever closer to the event horizon. They monitor the time at which the test mass passes them on its way deeper.

The observers use the global Schwarzschild time in their clocks.

The observers register that the test mass never reaches the event horizon. The word "never" is appropriate here, because the observers can synchronize their clocks in a perfectly sensible way and can make their clocks to run at the same rate. Any interval of time has the same duration measured by any of the clocks.

It is as if the observers were in the flat Minkowski space and they would use standard clocks.

          • ------>           ●              ●               ●

    photon                           observers

           ------------------> x

Imagine that the universe is the Minkowski space, and we have an infinite sequence of observers at ever larger distances from us. We send a photon along the x axis, and the observers monitor in the global Minkowski time when it passes them. The observers register that the photon never leaves the universe.

Does it make sense to extend the Minkowski global time t and and the x axis to cover the time "past the infinity"?

The proper time of the photon does not advance at all. We could say that the photon reaches the "edge" of the Minkowski space in a finite proper time. This is just like in the Schwarzschild metric, where the test mass reaches the event horizon in a finite proper time.

https://en.wikipedia.org/wiki/Non-standard_model_of_arithmetic

Extension past the infinity is a dubious thing. It is like changing the standard model of arithmetic to a non-standard model. We add on top of the natural numbers ℕ a copy of integer numbers ℤ.

Suppose that we in electromagnetism study a phenomenon where an electron comes ever closer to a certain position. Does it make sense to extend time past the infinity and calculate what the electron does after the infinite time has passed and it has reached that position? People would find the extension very strange.

Achilles and the tortoise

Photo George Hodan

https://www.publicdomainpictures.net/en/view-image.php?image=299670

https://en.wikipedia.org/wiki/Zeno%27s_paradoxes#Achilles_and_the_tortoise

The name of the tortoise coordinate refers to a claimed similarity of a test mass falling to a horizon and Achilles chasing the tortoise.

Is there a similarity?

Let Achilles and the tortoise run along the x axis. Achilles reaches the tortoise at x = 1.

Let us use synchronized clocks along the race path, such that the clocks agree about the duration of time intervals. The clocks will show that Achilles reached the tortoise in a finite time. There is no similarity to a test mass falling to a horizon.

To get an infinite duration for the race, we should use clocks which run the faster, the closer they are located to x = 1.

Conclusions

Changing coordinates and extending history past an infinite time of Schwarzschild coordinates does not seem sensible.

Extended coordinates are used to get the interpretation that the event horizon is a one-way membrane. We have argued in previous blog posts that a one-way membrane breaks thermodynamics, and leads to the black hole information paradox.

A dubious procedure leads to a model which breaks basic laws of physics. We conclude that extending coordinates past the infinity does not make sense.

The singularity at the event horizon is not just a coordinate singularity. The existence of the singularity shows that the model which is used to derive the behavior close to a horizon is bad. One cannot deduce the behavior of a test mass just from the Schwarzschild metric when the test mass is extremely close to the horizon.

Unusual causal structure in general relativity is evidence against its correctness

In our previous blog posts we wrote that (linearized theory) gravitational waves seem to allow one to travel back in time. That would bring all the time travel paradoxes, and be strong evidence against the correctness of general relativity as a physical theory.

https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.37.215

It turns out that Roger Penrose observed the problematic causal structure back in 1965.

"The following remarkable property is then obtained. No spacelike hypersurface exists in the space-time which is adequate for the global specification of Cauchy data."

Roger Penrose writes in the abstract of the paper that one cannot specify the initial values (Cauchy data) on a spacelike hypersurface.

https://arxiv.org/abs/hep-th/0211195

Veronika E. Hubeny and Mukund Rangamani (2002) state that "even the causal structure of pp-waves is different from that of flat spacetime."

https://en.wikipedia.org/wiki/Pp-wave_spacetime

A serious flaw in a physical theory is considered an exciting opportunity for science fiction

It is conspicuous that authors seem to consider a strange causal structure as "remarkable" or "interesting", rather than start to question the validity of the theory. If one would introduce a theory of electromagnetism which has a unusual causal structure, people would immediately suspect that the theory is flawed.

The Gödel metric, which has circular causal paths, is another instance where one should start to think if general relativity is broken.

In the Kerr metric there are circular causal paths, like in the Gödel metric.

Wormholes and the Alcubierre drive are other examples where circular causal paths appear.

People seem to hope that a time machine or a warp drive exists, even though it would make the physical theory contradictory.

The global Minkowski space c sets the speed limit in physics - not the local speed of light

UPDATE January 27, 2022: We removed our claim that the static electric field would move faster than light in a dielectric medium, like glass. The field presumably can move faster than light in a zone where the polarization capacity of the medium is "saturated". We do not know currently how far this zone extends.

----

It is not clear to us what the speed limit of physics is supposed to be in general relativity. How fast does the geometry of spacetime react to changes in the mass distribution?

We have already argued that the local speed of light around a black hole does not set any speed limit for a falling spherical shell. Nor does it restrict the speed of a very large falling mass.

The logical guess is that the universal speed limit of physics is the speed of light in the underlying true geometry of spacetime: the Minkowski space.

https://en.wikipedia.org/wiki/Cherenkov_radiation

An electron which moves faster than the local speed of light in water produces blue Cherenkov radiation. An analogous effect must happen in gravity if a point mass M speeds past the local speed of light.

A spherical shell falls very fast into a black hole: Galileo Galilei was wrong

Our January 17, 2022 blog post claimed that an elephant can run fast through a pool of syrup, which means that the merger of two large masses M can happen very fast in the global Minkowski time. The elephant "drags the frame" with it, and can move fast.

Our January 19, 2022 post about Birkhoff's theorem asked if the collapse of a spherical shell to a black hole happens extremely slowly. A shell cannot drag the frame.

It turns out that the collapse of a shell happens even faster, not slower.

A point negative charge approaches a central positive charge

Let us analyze the collapse in electromagnetism, so that general relativity does not confuse our thinking.

            •  ---->                    ● +

           e-                            

If a single electron approaches a central positive charge, the inertia of the electron is larger than in empty space for two reasons:

1. The electron is transporting the negative potential energy it has in the field. More displacement of energy => more inertia.

2. When the electron approaches, more energy from the field is shipped over a large distance to become kinetic energy of the electron. The distance seems to be the distance between the electron and the positive charge.

A spherical shell of negative charge approaches a central positive charge

                      -      -

              -                     -

          -                             -

          -  --->      ● +         -

          -                             -

              -                     -

                      -      -

Let the negative charge form a symmetric shell around the central positive charge. When the shell approaches the central charge:

1. It is not clear if the negative potential energy moves at all. The field outside the shell has lost energy. The outside field does not change when the shell moves closer.

2. The shell acquires kinetic energy by reducing the field at it, as the shell moves closer. A) Energy is shipped only over an infinitesimal distance? B) Alternatively, energy is shipped from the central positive charge?

It looks like the inertia of the shell does not grow at all, if 2. A is the case. The shell collapses fast. If 2. B is true, then inertia slows down the fall, but not as much as in the case of a falling point charge.

Our analysis suggests that the collapse of a spherical star into a black hole happens very quickly in the global Minkowski time, even faster than the merger of two equal-sized black holes. There is no "floating" of the shell close to the horizon. The floating effect only happens for a small point mass.

A symmetric shell seems to skip general relativity phenomena which are caused by increased inertia. As if there were no syrup.

If we send an expanding spherical shell outward, it will escape the black hole as easily. However, there is a problem. The shell moves faster than the local speed of a single photon. Is it possible to send the light shell?

General relativity in 1 + 1/2 dimensions

Working with spherical shells is doing physics with the time dimension and the positive half of the radial coordinate r. We could call this physics in 1 + 1/2 dimensions.

General relativity in 1 + 1/2 dimensions is presumably much simpler than in 1 + 3 dimensions.

We need to check what people have found out about general relativity in 1 + 1 dimensions. How much simpler are the phenomena which are due to increased inertia?

Galileo Galilei was wrong in 1638

https://en.wikipedia.org/wiki/Galileo's_Leaning_Tower_of_Pisa_experiment#/media/File%3APisa_experiment.png

Galileo Galilei claimed in his book in 1638 that all objects fall at the same speed in a gravity field, in vacuum. Our observation shows that he was wrong. A spherical shell, even of an infinitesimall mass, falls much faster into a black hole than a point mass does.

Drawing by Theresa Knott https://commons.wikimedia.org/wiki/File:Pisa_experiment.png#mw-jump-to-license

Also, our elephant in a syrup model shows that very heavy objects fall much faster than lightweight objects.

What is this about? This is about tidal effects. Tidal effects do not occur at all when a spherical shell falls. For a point mass, tidal effects have a huge influence on how it behaves in a very strong gravitational field. By tidal effects we mean anything that happens because of spherical asymmetry.

Since Birkhoff's theorem assumes full spherical symmetry, it is immune to tidal effects. However, one can ask what does the Schwarzshild metric in the theorem mean? Shells do not obey it at all. We have to investigate this.

Why there exist no longitudinal waves in otherwise empty space?

By changing the pressure of a spherically symmetric mass we can vary the pull it has on a point test mass m, if m is located inside the spherical mass.

One may ask if such a radial, changing force can create longitudinal gravitational waves in space.

We do not think longitudinal waves are possible. The mechanism which seems to create transverse waves is that far parts of the field of some charge q should move faster than light to keep the static field in the usual form. There must be some "transverse" movement of q.

But if q moves directly toward us, we can keep its static field in the usual form without any faster-than-light movement.

The origin of transverse waves is in the lagging of the far field.

We have also remarked that the finite speed of light can simulate inertia in transverse movements of field lines. A wave requires some kind of inertia, or a delay, to exist.

It is harder to imagine how a longitudinal movement of a field line could simulate inertia.

If space is not empty, but contains plasma, then longitudinal waves can propagate. They get the required inertia from the plasma.

Birkhoff's theorem requires the use of a spherical shell as the test mass

UPDATE January 20, 2022: Is the spatial metric inside a spherical shell not stretched? If we simply add linearly the metric perturbations caused by each particle in the shell, the spatial metric must be stretched inside the shell. The speed of light is the same to all directions, but distances might have uniform stretching? We have to check the literature, and analyze the metric inside a spherical shell.

At the first sight, linearly adding perturbations is not the right way, because energy shipping happens in the combined field of the mass shell. The spatial metric is not stretched. So, no problem.

We also removed the incorrect claim that pressure inside a spherically symmetric mass can attract a point test mass outside the mass.

----

In our November 6, 2021 blog post we were worried that Birkhoff's theorem may be broken, because varying pressure inside a spherically symmetric mass may vary tidal forces on a point test mass m outside the spherical mass. Thus, the metric, as seen by a point test mass, can change outside a spherically symmetric mass. Is Birkhoff's theorem broken?

Now we realize that one must use a spherical shell of mass as the test mass in Birkhoff's theorem. A point test mass m would break the spherical symmetry of Birkhoff's theorem.

A spherical shell test mass does not cause tidal forces.

Is a spherically symmetric collapse to a black hole extremely slow?

In the syrup model of gravity on January 17, 2022 we remarked that an elephant can run fast through the syrup. That is, the merger of two equal-sized large masses happens very fast.

A large mass drags the frame with it and can move much faster than a small particle.

But in a spherically symmetric collapse there probably is no frame-dragging. If a spherically symmetric system of electric charges collapses, there is no magnetic field. On the other hand, a speeding single charge has a significant magnetic field.

We argued that even a 1 MeV photon passes the event horizon quickly, because it cannot acquire more inertia than exists in the whole black hole. The argument does not work well with a contracting shell of mass, because the total momentum of the shell is zero.

It might be that a spherically symmetric collapse into a black hole happens extremely slowly in the global Minkowski time. We need to study this. 

A test mass in a pressurized vessel: the metric according to our Minkowski & newtonian model

The interior Schwarzschild solution of incompressible fluid claims that increasing the pressure in a central part of a sphere only changes the metric of time, and cannot change the metric of space.

https://en.wikipedia.org/wiki/Interior_Schwarzschild_metric

We have suspected for several years that the rigidity of the spatial metric under pressure cannot be true. On November 20, 2020 we wrote about a perpetuum mobile which would exploit the infinite rigidity of the spatial metric.

It turns out that Karl Schwarzschild did calculate correctly back in 1916.

Let us have a test mass inside a spherical pressurized vessel. Below we estimate that moving the test mass radially seems to do the same amount of energy shipping as moving it tangentially.

The inertia of a test mass is the same for tangential and radial motion. Light moves at the same speed radially and tangentially, measured by an outside observer. That implies that time has slowed down, but there is no stretching of the radial or the tangential spatial distances.

A spherical pressurized vessel

On November 8, 2021 we calculated exactly that one can explain the potential of pressure at the center of the Schwarzschild metric simply by considering the spatial expansion which a test mass m causes in a spherical vessel.

        vessel, radius R

               ----------    

           /                  \

         |         <--- •      |  m test mass

           \                  /

               ----------

 

Suppose that we have a pressurized spherical vessel, and we move a test mass from its side to the center. The volume of the vessel expands. We can harvest energy from the movement of m.

Thus, m has a "potential" in the vessel. The potential is the lowest at the center.

Where is the (negative) potential energy of m located?

The spatial metric is stretched close to m. If m moves at almost the speed of light, the negative energy is presumably close to m. We assume that the fluid does not have time to adjust to the change in the metric.

The negative potential energy then is very clearly localized: it is in those parts of the vessel whose volume m has increased. Pressure did work when space expanded.

Estimating the energy displacement

Let us model the stretching of the spatial metric with concentric, overlapping, spheres around m. Each sphere may represent, say, 0.1% of stretching. How much energy is shipped if we move such a sphere A a short distance s radially or tangentially? Let us denote the radius of A by R'.

        vessel, radius R

               ----------    

           /                  \

         |              O      |  sphere A, radius R'.

           \                  /

               ----------    

If the sphere A fits entirely inside the vessel, then, of course, the energy shipping is the same if we move A radially or tangentially. In the diagram, O denotes the small sphere A.

If A is so large that the whole vessel is inside A, then there is no energy shipping inside the vessel. We ignore the effect on the walls of the vessel and only calculate energy shipping inside the vessel.

                                                        X

                                                         X

                  • <-- r --> × <----- R -----> X

              s  |                                     X

                  v                                   X

    test mass m     center          energy E

If

       R' = R,

and m is at a small distance r from the center × of the vessel, then moving m tangentially rotates the energy E (marked with XXXX) at the edge of the vessel on the opposite side. If we move m tangentially a distance s, then we move E a distance

       s R / r.

The energy displacement is

       E s R / r.

If we move m the distance s < r right, we ship the energy E s / r to the left to the test mass m, over a distance

       R + r,

which is approximately R since r is small. The energy displacement is

       E s R / r.

The displacements agree for a radial and a tangential motion.

If

       R' = R + k,     0 < k,

and k is not large, then the case is very roughly symmetric to the case

       R' = R - k.

A radial movement does do more energy displacement in the case R + k, but does about the same amount less in the case R - k.

We presented extremely crude arguments that suggest that the energy displacement is the same in a tangential and a radial movement. A precise calculation can be done with a computer, or it might be possible even analytically.

General relativity has an exact analytical result in the Schwarzschild internal metric. Our Minkowski & newtonian model agrees with general relativity about the potential caused by pressure. We believe that general relativity and our model agree about the spatial metric, too.

Why the November 20, 2020 perpetuum mobile does not work? The problem of conservation laws

              ----------    

           /                  \

         |         ● M ----------------->

           \                  /

               ----------

Let us have an extremely rigid vessel which we fill with almost incompressible fluid.

We put a mass M at the center of the vessel. The volume of the vessel grows and we pour in more fluid.

The pressure in the vessel is zero, and M does not feel any pull of gravity.

We then shoot M out at almost the speed of light. Since M moves so fast, it does "know" what is happening behind it. The volume of the vessel shrinks and we can harvest huge energy from the pressure.

Why the process does not work? How does M know that it is not allowed to fly out?

We may further assume that M is a pulse of light. Is the light reflected back?

There are probably many similat settings where a light-speed object seems to break conservation of energy or momentum. We have contemplated the question of conservation laws, but have not yet found a good model which would enforce them.

We suggested that in quantum mechanics, processes are "transactional". An unknown central authority checks that conservation laws are obeyed before approving a transaction.

If we believe in the existence of fields, then the field of M must linger inside the vessel, even though M itself is speeding away. How can the field "tell" M that it should stop?

The question is clearly about the self-force of a field on the particle itself. Can the field communicate superluminally with the particle?

This question is arguably the greatest open problem in theoretical physics. We will keep trying to solve it.

Demystifying gravity: a summary of our results so far

There is an overarching theme which appears in all our results about gravity so far: we show that gravity does not possess certain strange features which some 20th century physicists claimed it to have.

Let us recapitulate:

1. Gravity does not change the true Minkowski geometry of spacetime. Gravity only simulates a changed metric, for small masses, and rods which are not very rigid. "Time itself" has not slowed down. It is certain clocks which run slower. The illusion of a changed metric is a side effect of the newtonian force field.

2. Gravity does not hold a special status among forces. Electromagnetism contains analogues for all the phenomena of general relativity.

3. Gravitational waves are newtonian force field waves. They are analogous to electromagnetic waves. The apparent change of the metric in a gravitational wave is a side effect of an ordinary wave of a force field.

4. Travel back in time, or faster-than-light travel, is not possible with gravitational waves, nor by any other means. The Alcubierre drive cannot work.

5. The event horizon of a black hole is not a one-way membrane. Light can come up through it.

6. Black holes do not break rules of thermodynamics.

7. Hawking radiation does not exist. Black holes radiate ordinary radiation, which can be thermal or nonthermal. There is no information paradox, nor a black hole firewall.

8. There are no singularities in black holes.

9. There are no white holes or wormholes.

10. Quantum theory of gravity is not fundamentally different from quantum electrodynamics.

What remains? Are there any other strange features of gravity that we should refute?

In cosmology, people believe that there is a singularity at the start of our universe. We will look into that question.

The inflation hypothesis claims that gravity can create energy from nothing through a hypothetical inflaton field. The claim is suspicious. In an ordinary explosion, one cannot create energy from nothing. We will look at this.

The dark energy hypothesis is similar to the inflation hypothesis.

Is the Einstein-Hilbert action incorrect or do people interpret it in a wrong way?

https://en.wikipedia.org/wiki/Einstein%E2%80%93Hilbert_action

It may be that the Einstein-Hilbert action does calculate the combined effect of gravity and electric forces correctly. The error may have been that people believed that the metric is the "spacetime geometry" which all objects must obey like slaves. The action looks quite innocent. It should not force anyone to act as a slave.

We will investigate this in detail. For example, why does the interior Schwarzschild metric claim that the spatial metric stays the same regardless of the applied pressure? The stubbornness of the spatial metric is suspicious.

As far as we know, no one has solved the Einstein-Hilbert action for a particle falling into the event horizon of a black hole. It may be that once one solves the action correctly, taking into account the backreaction of the system to the particle, the results agree with our Minkowski & newtonian model.

https://en.wikipedia.org/wiki/Geodesics_in_general_relativity

The principle that small particles follow geodesics of the metric is usually taken as an axiom in general relativity. But the status of the axiom is still being debated.

When a particle falls into an event horizon, the backreaction may be significant.

There cannot be a singularity at the center of a black hole - no quantum mechanics is needed

Singularity theorems by Roger Penrose require that a closed trapped surface forms.

https://en.wikipedia.org/wiki/Penrose%E2%80%93Hawking_singularity_theorems

The definition of a closed trapped surface is the following: if light is sent from the surface to all directions, then after some time, all the photons are in a "volume" which is smaller than the volume enclosed by the original surface.

A closed trapped surface is, in a sense, a one-way membrane. We argued in our previous blog post that one-way membranes cannot exist because they would break a time symmetry of nature, and break thermodynamics.

We conclude that the assumptions of the Penrose singularity theorems are never met. They are void theorems. The 2020 physics Nobel committee did not realize this.

Can a singularity form in a classical collapse?

Let us ignore quantum mechanics. If we have point masses under the attraction of gravity, can they collapse into a singularity?

Let us assume that we have just two point particles which orbit each other. The particles do not have any other interaction but gravity.

Let us measure energies as seen by a distant observer. The amount of energy of a system is defined by how much a distant observer would receive if the energy were sent to him.

The particles keep orbiting and losing their energy in gravitational radiation. What is the final state?

The gravity charge of the particles grows smaller. There is nothing that would stop the process. A faraway observer sees the system having less and less mass-energy.

Thus, the final state is not a singularity, but a very lighweight system which keeps orbiting and radiating. The particles have to be very close to each other, so that their potential reduces the mass-energy to a low value.

The effect of quantum mechanics

A distant observer sees the particles very lightweight at the end. Does an uncertainty principle prohibit them from coming very close to each other?

A local observer sees the particles still having their original mass. His uncertainty principle allows the particles to come closer than the principle of the distant observer.

Which observer is right?

An equivalence principle suggests that the local observer has the correct view of things.

Anyway, quantum mechanics stops the particles from coming closer. The system has a lowest energy state. In an earlier blog post we suggested that the final state is a "crystal". The lowest energy state of two particles is, in a sense, a crystal.

The Shwarzschild radius or "event horizon" is the place where the "viscosity" of gravity becomes extremely large

We have argued that light can always escape from a black hole. There cannot be a one-way membrane. What is the relevance of an event horizon then?

We get a clue from the Schwarzschild metric just outside the Schwarzschild radius r_s. Light propagates extremely slowly there.

We argued in our October 20, 2021 blog post that a 1 MeV photon can still fall through the event horizon of a solar mass black hole in less than 1.38 milliseconds. Light does not stand completely still.

The event horizon is the radius where the "syrup" of the gravity field becomes extremely viscous. Light moves at a tiny fraction of its normal speed.

We conjecture that light propagates at roughly the same tiny velocity within the event horizon. The viscosity of the syrup is roughly the same inside.

Photo https://www.publicdomainpictures.net/en/view-image.php?image=47609

In a syrup, small animals can only move very slowly. But an elephant whose mass is equal to the pool of syrup can still run fast through it.

In gravity, the situation is the same: if we drop a mass M to a black hole whose original mass is M, then the falling mass will move very fast, since it cannot acquire large inertia in the field of the black hole. Small masses will move extremely slowly when they reach the event horizon.

The elephant is another instance of our claim that gravity can create the illusion of "spacetime geometry" for small masses, but not for very large masses. A photon moves very slowly, but a large mass runs through at a large velocity.

Conclusions

There cannot be a singularity inside a black hole. This is true both in classical physics, and in quantum mechanics.

We conjecture that the Einstein-Hilbert action does not lead to singularities, when interpreted correctly. The claim that singularities form comes from the misunderstanding that the geometry of spacetime is "infinitely strong".

Albert Einstein never believed in the existence of black holes, and tried to prove that they cannot form.

https://en.wikipedia.org/wiki/Einstein%27s_unsuccessful_investigations

In his 1939 paper he claimed that a collapsing system spins so fast that it cannot contract below the Schwarzschild radius.

Now we see that Albert Einstein was on the right track. However, the system does contract below the Schwarzschild radius. But the spinning prevents a central singularity from forming.

The event horizon: general relativity breaks a time symmetry of laws of nature

Let us have a system of particles which attract each other. How to define the "potential" at a certain location?

Having a test mass m with "negative energy" in a "potential"

We can use a rope to lower a test mass m to a location in the system, and measure how much energy we can harvest. Let us assume that we were able to harvest more energy than m c². Is that a problem? Do we have now an object with negative mass-energy?

We may imagine that the forces between particles are complex. Maybe we have mechanical robots in the system, and they pull certain test masses so vigorously that we can harvest more than m c² of energy when lowering the test mass down. Having such robots does not introduce any fundamental problem. Having "negative energy" for a test mass does not lead to any paradox.

On the other hand, the energy of the whole system cannot become negative, since then we would have all the paradoxes of negative energy objects.

An old problem is how to localize the energy of a system of particles. If we harvest the binding energy when we build the system, from where is that energy missing?

If we have a very rigid shell of mass, the potential of each of its parts may be close to -m c², but the binding energy of the shell is only 1/2 of the negative potential energy. Thus, the shell has large mass-energy. Where is that energy located?

It may be a wrong approach to try to assign the energy of a complex system to its parts.

The Schwarzschild metric within the event horizon is strange: it breaks a time symmetry of laws of nature, as well as thermodynamics

https://en.wikipedia.org/wiki/Schwarzschild_metric

In the Schwarzschild metric formula,

       r_s = 2 G M / c²

is the Schwarzschild radius. It is the radius of the event horizon in the standard Schwarzschild coordinates. M is the mass of the spherically symmetric object, as measured by a faraway observer.

In general relativity, the event horizon is a one-way membrane. The metric inside the event horizon is strange. If we in the formula above have r < r_s, the signs of the time metric and the radial metric flip. When the proper time τ of an observer increases, his radial coordinate r must decrease. The metric claims that all objects must approach the center?

Actually, the metric says that the radial coordinate r must change: the formula just says that dr² must be nonzero. People usually think that r must decrease, but is it really so?

Just above the event horizon the metric says that the force of gravity, as seen by a static local observer, tends to infinity. If the photon does not move outward exactly radially, gravity will pull it to the event horizon. Since no photon moves exactly radially, the event horizon is a one-way membrane.

In traditional classical physics it would require an infinite force to ensure that all objects will approach the center.

In our Minkowski & newtonian model, gravity is about inertia and Newton's gravity force, which is analogous to the Coulomb force. We cannot make a one-way membrane in electromagnetism. Thus, it should not be possible in gravity either.

The metric for r ≤ r_s is not compatible with the Minkowski & newtonian model. On the other hand, the metric for

       r > r_s + ε

is just what the Minkowski & newtonian model predicts, where ε is some very short distance which depends on M.

One can simulate the metric for r > r_s with a finite force, but for r = r_s it would require an infinite force.

After Albert Einstein introduced general relativity in 1915, some people criticized the apparent singularity at r = r_s. The critics were right. 

Having infinite forces is unnatural. They break a time symmetry of laws of nature: a certain process can only happen to one direction.

A one-way membrane breaks thermodynamics, too. Jacob Bekenstein and Stephen Hawking realized this, and tried to fix general relativity. They did not realize that the error is in general relativity itself, and one cannot remove the problem with Hawking radiation.

Where is the flaw in general relativity?

For thermodynamics to work, physical processes cannot be just one-way. Having a one-way membrane in the event horizon is a major flaw in general relativity.

What is the root cause for the one-way nature of general relativity?

One of the reasons is that people think that the "geometry of spacetime" is something which has "infinite strength". Even a small mass M can make an infinitely strong geometry around itself.

General relativity, as understood by most people, has a similar infinite strength problem in gravitational waves. People think that the waves fundamentally change the "geometry of spacetime" in their zone. However, as we have argued, the waves only have finite energy. They cannot significantly change the geometry as seen by very large masses and very rigid rods. The true Minkowski space geometry is hiding below the wave which only has finite energy.

Is the flaw in the Einstein-Hilbert action, or is it just in its interpretation in the study of black holes?

There is some kind of a lagrangian or a hamiltonian behind the Einstein-Hilbert action. One would expect that a process in a typical hamiltonian cannot be just one-way, since that would require an infinite force.

We conjecture that the flaw is in an incorrect interpretation of the Einstein-Hilbert action. 

A correct interpretation would not involve a one-way event horizon. The fact that general relativity treats gravity in a way different from other forces is a contributing factor in the wrong interpretation. For an ordinary force, one would immediately suspect a calculation error if one would get infinite forces.