UPDATE August 26, 2023: The problem in this particular case was not in bulging coordinates, after all. The Einstein approximation formula miscalculates the Lorentz transformation of the static metric into the moving frame. That is why it does not agree with the Lorentz transformation of the acceleration. Bulging coordinates cause problems in other configurations.
Also, the equations of general relativity probably do respect Lorentz covariance. The error is in the Einstein approximation formula.
----
UPDATE August 23, 2023: We probably found the problem. The problem was what we already pointed out on August 15, 2023: the Einstein-Thirring coordinates are error-prone because the coordinate lines "bulge" around a mass M, relative to the Schwarzschild coordinates. The acceleration against moving bulging coordinates is non-zero while it would be zero in orthogonal coordinates.
-----> grid moves right
Imagine a static observer (marked with x) in the upper half of the image above. If we move the coordinate grid to the right, the y coordinate value for the observer will change with time: there is a spurious y acceleration which is a result from a poor choice of coordinates.
We have to analyze what implications this has. We have been using Schwarzschild coordinates, while gravitoelectromagnetism uses Einstein-Thirring coordinates.
Also, a Lorentz transformation between bulging coordinates probably fails. That may be the ultimate error: the transformation of an acceleration between moving bulging coordinates is not a Lorentz transformation.
If Einstein and Thirring calculate for two moving masses M1 and M2, the bulges are different in the coordinates of M1 versus the coordinates of M2. Summing the metric perturbations may be nonsensical.
The Schwarzschild coordinates is what we get if we make a 3-dimensional model of the 2-dimensional spatial metric around M, and project the surface (Flamm's paraboloid) on a 2-dimensional plane which asymptotically runs parallel to the model. We could take as an axiom in general relativity that one must sum perturbations using such projected coordinates. That would make the Schwarzschild coordinates canonical.
In our own Minkowski & newtonian gravity model, the Schwarzschild coordinates are canonical because they are canonical coordinates for the underlying Minkowski space. In our model, spacetime is not curved, but it is the measuring devices whose behavior changes when they are in a gravity field. A mechanical clock ticks slower and a ruler pointed into the radial direction shrinks in length when they are close to M.
----
We will use the Einstein approximation formula and calculate in the laboratory frame and a comoving frame of a moving mass M. We will show that we get different values for the acceleration, which proves that the method is not Lorentz covariant.
We set the speed of light c = 1.
Einstein, Albert, Näherungsweise Integration der Feldgleichungen der Gravitation, June 22, 1916.
The metric and its derivatives in the laboratory frame
M ● ---> v
R = distance (m, M)
m • ---> v
^ y
|
--------> x
A mass M moves to the right at the velocity v. We have a test mass m located below M, a distance R down, moving in unison. In the laboratory frame the mass M includes the kinetic energy.
Let us calculate γ'_μν as a function of R_m at the location of the test mass. The "mapped" stress-energy tensor
∫ T_μν(...) / r * dV₀
only contains a non-zero component M for the time coordinate t for the x momentum. It is of the form:
M / R M v / R 0
M v / R 0 0
0 0 0
The first Einstein formula above calculates the perturbation h of the Minkowski metric by "trace reversing" the mapped stress-energy tensor. We need to flip some signs in order to switch to the (- + +) sign convention which we use. Einstein uses a (+ + +) convention.
h = 4 G *
1/2 M / R -M v / R 0
-M v / R 1/2 M / R 0
0 0 1/2 M / R
The full metric is the above perturbation h summed to the Minkowski metric:
η =
-1 0 0
0 1 0
0 0 1
The y acceleration of the test mass in the laboratory frame
Above, ds is a time interval dτ of the proper time of the the test mass m. The index μ is y. Both gravity and the velocity v affect the proper time τ of m. We denote:
dτ / dt = C.
C is slightly less than 1. We have
dx_x / dτ = dx / dt * dt / dτ
= v / C,
dx_t / dτ = dt / dτ
= 1 / C,
dx_y / dτ
= 0.
The y derivatives:
d g_tt / dy = 2 G M / R²,
d g_xx / dy = 2 G M / R²,
d g_tx / dy = -4 G M v / R².
In the geodesic equation we sum over the combinations (α, β) = (t, t), (x, x), (t, x), (x, t). Then:
Γ_ytt = -1/2 d g_tt / dy
= -G M / R²,
Γ_yxx = -G M / R²,
Γ_ytx = Γ_yxt
= 2 G M v / R².
To raise the y index in Γ_y... we have to multiply the values above by
1 / g_yy = 1 - 2 G M / R.
Then
d²y / dτ²
= 1 / g_yy * ( G M / R² * 1 / C²
+ G M / R² * v² / C²
- 4 G M v / R² * v / C²),
and, since dτ = C dt,
a
= d²y / dt²
= (1 - 3 v²) * 1 / g_yy * G M / R².
The y acceleration of the test mass in the comoving frame
Let us switch to a comoving frame of M. The mass M' is less by the kinetic energy in that frame:
M' = (1 - 1/2 v²) M.
Since the M' is less, the corresponding g_yy term is slightly different:
1 / g'_yy / 1 / g_yy
= 1 + v² G M / R.
We can ignore the difference if M is small. In the comoving frame we have
a'
= d²y / dt'²
= 1 / g_yy * G M' / R²
= (1 - 1/2 v²) * 1 / g_yy * G M / R².
Above,
γ_v² = 1 + v²,
and v • u' = a' • v = 0.
The mapped acceleration in the laboratory frame is
(1 - 3/2 v²) * 1 / g_yy * G M / R².
It differs from the value which we calculated in the laboratory frame!
If we believe that the Schwarzschild metric in the comoving frame is correct, and that Lorentz transformations work, then the acceleration derived in the comoving frame is the correct one. Einstein's approximation calculates incorrectly in the laboratory frame.
Could this be a problem in the linearization of general relativity?
The relative error in the acceleration in the two calculation frames is
(1 - 3 v²) / (1 - 3/2 v²)
= 1 - 3/2 v²,
the absolute error is linear in M.
Suppose that the nonlinearity of the full Einstein equations somehow heals the problem by introducing some correction. But we expect general relativity to approach a linear theory when M goes to zero. Then the correction, relative to M, should go to zero. It should not be linear in M.
It is likely that the full Einstein equations breach Lorentz covariance.
Can we make general relativity Lorentz covariant by requiring that we calculate in the center of mass frame?
^ v ^ v'
| |
• m ● M
Consider a configuration where there is a large mass M very far away, and we are interested in what happens in the vicinity of a much smaller mass m. The field of M near m is negligible.
If the canonical frame is fixed to M, then general relativity would calculate wildly different values near m, depending on the movement of M very far away. This does not seem right.
Our own method is Lorentz covariant
Our own calculation method for the orbit of a test mass is Lorentz covariant for weak fields:
1. we choose the comoving frame of a mass particle as the canonical frame;
2. we calculate corrections to the newtonian acceleration of a test mass in the canonical frame, using the Schwarzschild metric for the particle;
3. we Lorentz transform the corrections to the laboratory frame and sum them for all the mass particles.
Let us prove the Lorentz covariance. Let the sum of corrections be
a(f₁)
in a frame f₁. We have to show that
a(f₂) = Λ_f₁f₂ ( a(f₁) ),
for another frame f₂, where Λ_f₁f₂ is the Lorentz transformation between frames
f₁ --> f₂.
The conclusion follows trivially from linearity and transitivity:
Λ_f₁f₂ (a + b) = Λ_f₁f₂ (a) + Λ_f₁f₂ (b),
Λ_f₂f₃ ( Λ_f₁f₂ (a) ) = Λ_f₁f₃ (a).
Conclusions
The fact that general relativity breaks Lorentz covariance was probably discovered immediately when general relativity was introduced in 1915. People must have tried to prove the Lorentz covariance, but failed. In the literature there are scattered mentions of breaching the Lorentz covariance.
"While Maxwell's equations are invariant under Lorentz transformations, the GEM equations are not. The fact that ρg and jg do not form a four-vector (instead they are merely a part of the stress–energy tensor) is the basis of this difference.[citation needed]"
Wikipedia is aware of a Lorentz problem, but the link to literature is missing. There seems to be no definite proof of the Lorentz failure written anywhere. Our blog post may be the first exact proof.
What people have not realized is that the Lorentz failure affects general relativity calculations of moving systems, in a major way. We get wildly varying numbers on frame dragging, depending on the frame which we choose.






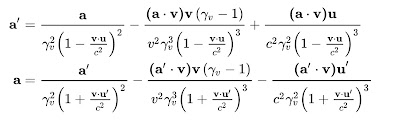
No comments:
Post a Comment