UPDATE November 12, 2023: The Kerr metric may be approximately correct close to a rotating very heavy mass M. Start from a nonrotating M and take the Schwarzschild metric. If we switch to a slowly rotating coordinate system, the effects of the centripetal acceleration are small and we ignore them. The coordinate speed of light close to M is very slow. In the new coordinates, we see M strongly fragging the frame along with it.
Our calculations in this blog have been about very weak gravity fields, and far away from M. The behavior close to a black hole may be qualitatively different.
----
Let us use our methods to determine the effect of rotation on a prograde circular orbit. We will calculate using the framework from August 10, 2023. We will try to check the correctness of the August 10 post by recapitulating the steps of the proof. Already on August 4, 2023, we tried to calculate the equatorial circular orbits. Now our understanding of Lorentz transformations is better and we should repeat the calculation.
We calculate for a thin equatorial disk whose radius is R₀. The disk rotates at an angular velocity ω. We want to know how the rotation affects the gravitational pull toward the center of the disk. In newtonian gravity there would be no effect from the rotation.
<---- ω
^ v''
\
dm''' • • dm''
/
v''' v
X center of ball
^ v
/
dm' • • dm
\
v' v
• -------> V
m
^ x
|
---------> y axes of the laboratory frame
In the diagram above we have four parts of the disk moving along with the rotation of the disk. The part dm' is mirror symmetric with dm against the line (m, X), and dm''' and dm'' are mirror symmetric to dm' and dm.
The test mass m is on a prograde circular orbit. We have v and V very small, and
v << V.
Switch to a comoving frame of m
R_m = distance (m, X)
X center of ball
| \
| \ R
| \
| \
α ● dm is static
r = distance (m, dm)
β angle (m, X) vs. (m, dm)
/
/
m • ---__
---> V' = V - v
Above, we switched to the comoving frame of dm. Just like on August 10, we argue that length contraction and time dilation are insignificant because v² is very small.
The Lorentz correction to V - v is roughly
~V * v V / c².
We can ignore it because its ratio to v is
~ V² / c²,
and by choosing V small, the ratio is extremely small. However, we have to check that this minuscule error does not somehow get magnified below.
Let us decompose V' into a radial velocity vector which points toward dm:
v_r = V sin(β) - v sin(α + β),
and the tangential velocity orthogonal to it:
v_t = V cos(β) - v cos(α + β).
The radial Schwarzschild and Lorentz corrections
The gravity field of dm is very weak and v and V are very slow. Then the acceleration in the comoving frame of dm is almost exactly the newtonian:
a' = G dm / r².
Let us first calculate the Schwarzschild correction which results from the radial movement of the test mass m, in the direction of dm.
From the August 10 blog post we see that the Schwarzschild correction formula for the radial acceleration from a radial movement is:
-v_r² r_s / r²
= - (V sin(β) - v sin(α + β))² r_s / r²,
where sin(β) is approximately
sin(α) R / R_m.
The term
V² sin²(β) / r² ~ 1 / R_m⁴,
and we can ignore it. We can also ignore the v² term. The remaining term is
2 V sin(β) v sin(α + β) r_s / r².
It is approximately
2 V sin(α) R / R_m * R ω sin(α)
* 2 G dm / c² * 1 / R_m².
To get the acceleration upward, we should multiply it by cos(β), but we assume that β is a small angle and the cosine is 1.
We have to integrate over 0 < α < π and 0 < R < R₀. The integral of sin²(α) is
π / 2.
The mass element for a thin equatorial disk is
dm = ρ dR R dα,
where ρ is the mass per area. We have to integrate
R₀
∫ 2 V G / c² * 1 / R_m³ ω ρ π R³ dR
0
= V G / c² * 1 / R_m³ * 1/2 ω R₀² ρ π R₀²
= V G / c² * 1 / R_m³ * 1/2 ω I
= V G / c² * 1 / R_m³ * 1/2 J,
where I is the moment of inertia of the disk, and J is its angular momentum. We have to double the value to take into account the left half of the disk.
A Lorentz transformation only changes that acceleration little. We map it directly to the laboratory frame.
The effect is to pull the test mass toward the rotating disk. The formula corresponds to a gravitomagnetic moment -J.
Next we will calculate the Lorentz correction from the newtonian acceleration a' toward dm, as we move back from the comoving frame to the laboratory frame. In a newtonian calculation there would be no Lorentz correction.
The vector u' in the formula is V' in our notation. The middle term for a' is ~ v², because γ_v - 1 ~ v², and we can ignore it.
The first and the third term depend on
v • V'
We can replace V' by V because the value of the terms only changes by ~ v². We can assume γ_v = 1 because it only differs from 1 by ~ v².
The first term brings a correction to the x acceleration:
-a' * 2 v • V / c² * cos(β).
The third term brings
-a' • v * V / c² * cos(β).
The third term for dm' has the sign flipped relative to dm. We can ignore the third term by symmetry.
The first term is
-G dm / r² * 2 v cos(α) V / c² * cos(β).
It is almost canceled by the corresponding term for dm''.
The factor 1 / r² is smaller for dm'' approximately by
-2 / r³ * 2 R sin(α).
The sum of the first term for dm and dm'' is approximately
-8 G / c² * 1 / R_m³ * R sin(α) v cos(α) V cos(β) dm.
We can treat cos(β) = 1 for large R_m. The mass element for a thin equatorial disk is
dm = ρ dR R dα,
where ρ is the mass per area. We have to integrate over 0 < α < π / 2 and 0 < R < R₀. The integral
π / 2
∫ sin(α) cos(α) dα = 1/2.
0
We still have to integrate
R₀
∫ -4 G / c² * 1 / R_m³ * R * R ω V ρ R dR
0
= -V * G / c² * 1 / R_m³ * 1 / π * R₀² ρ π R₀² ω
= -V * G / c² * 1 / R_m³ * 1 / π * I ω
= -V * G / c² * 1 / R_m³ * J / π,
where I is the moment of inertia of the disk, and J is its angular momentum. We have to double the value since the left side of the disk contributes equally. The correction corresponds to a gravitomagnetic moment 2 / π * J.
The effect is to pull the test mass away from the rotating disk.
Corrections from the radial movement of m on the tangential movement of m
In the comoving frame, the test mass m moves toward dm at a speed
v_r = V sin(β) - v sin(α + β).
That slows down the tangential speed of m relative to dm, because in the Schwarzschild metric around dm,
where h is the constant specific angular momentum, μ = m is the reduced mass, dφ is the change in the Schwarzschild polar coordinate, and dτ is a short proper time of the test mass.
For a newtonian orbit,
r² dφ / dt
is constant. Let us compare the newtonian orbit and the Schwarzschild orbit.
We assume that the test mass starts from a certain point P at a velocity V, which is measured in Schwarzschild coordinates.
We assume that the test mass moves closer to dm. Compared to the newtonian orbit, in the Schwarzschild orbit dφ / dt slows down because τ slows down relative to t:
dφ / dt = dφ / dτ * dτ / dt.
Let the test mass m descend a short distance Δr lower in a time Δt. Proper time for a static observer there runs slower because it is a lower potential. Also, the test mass gains kinetic energy, which slows down its proper time.
The slowdown from the potential is calculated from
sqrt(1 - r_s / (r - Δr))
= 1 - 1/2 r_s / (r - Δr)
= 1 - 1/2 r_s / r - Δr * 1/2 r_s * 1 / r²,
where
Δr * 1/2 r_s * 1 / r²
= 1 / m * m * Δr * G dm / c² * 1 / r²
= W / (m c²),
where W is the work of gravity on the test mass m as it descends Δr.
The slowdown from the increase in kinetic energy is (ΔV is the change in the velocity):
1 / sqrt(1 + (V + ΔV)² / c²)
= 1 - 1 / m * m * 1/2 (V + ΔV)² / c²
= 1 - E_kin / (m c²).
As the kinetic energy E_kin increases by W, the slowdown is
W / (m c²).
The end result is that the tangential component v_t of V slows down, relative to the newtonian orbit,
2 W / (m c²)
in a time Δt = Δr / v_r, where v_r is the radial component.
The tangential acceleration correction is
a_t = -v_t * 2 W / (m c²) * v_r / Δr
= -v_r v_t * 2 F / (m c²)
= -v_r v_t * 2 G m dm / r² * 1 / (m c²)
= -v_r v_t r_s / r².
We obtained the same formula as on August 10. Recall from above:
v_r = V sin(β) - v sin(α + β),
v_t = V cos(β) - v cos(α + β).
We will study below the four terms in -v_r v_t r_s / r²:
- V² sin(β) cos(β) r_s / r²
+ V sin(β) v cos(α + β) r_s / r²
+ V cos(β) v sin(α + β) r_s / r²
- v sin(α + β) v cos(α + β) r_s / r².
Do Lorentz transformations of the four tangential acceleration terms bring in corrections?
The terms are accelerations in the comoving frame of dm, normal to (m, dm). We have to check if Lorentz transforming these into the laboratory frame brings in anything new. We recapitulate the Wikipedia formulae:
We can replace V' by V because the value of the terms only changes by ~ v².
The first term V² sin(β) cos(β) r_s / r² would dominate because V >> v, but we eliminate it by summing to the corresponding term for the mirror image dm': sin(β) has the opposite sign for dm'. It would cancel entirely without Lorentz corrections.
Looking at the Wikipedia acceleration formulae above, the Lorentz correction to a tangential acceleration a' is approximately the factor (since a' and V are roughly parallel):
-a' (3 v • V / c²),
The Lorentz correction differs for dm and dm'. The sum of the corrected first term for dm and dm' is then at most
6 |v| |V| / c² * V² sin(β) cos(β) r_s / r².
If we choose v and V very small, the sum is negligible relative to the radial corrections above.
The second term V sin(β) v cos(α + β) r_s / r² we reduce by summing it to the corresponding term for dm'', where dm'' is the mirror image of dm as in the diagram above. Then cos(α) has the opposite sign for dm'', but the 1 / r² term causes a difference.
The sum (= acceleration) is something like
V v sin(β) cos(α + β) * 2 R r_s / r³
without the Lorentz transformation. There sin(β) ~ 1 / R_m. The formula is ~ 1 / R_m⁴, and can be neglected altogether. No need to check Lorentz.
The third term is -V cos(β) v sin(α + β) r_s / r². Summing the contribution for dm' and dm would cancel the term entirely because the sine flips sign, but Lorentz corrections leave a remnant.
The first term in the formula above for a produces for a Lorentz correction for a tangential acceleration a':
-2 a' v V sin(α).
The second term is ~ v² and we can ignore it. In the third term, V' = V - v. The term for V produces a vector with a zero x component. The term with v is ~ v² and we can ignore it.
We have
-2 a' v V sin(α)
= -2 V cos(β) v sin(α + β) r_s / r²
* v V sin(α),
which is ~ v², and we can ignore it.
The fourth term v sin(α + β) v cos(α + β) r_s / r² is negligible if we choose v very small.
Tangential corrections are negligible. This is not surprising because Schwarzschild corrections associated with V, which is almost normal to (m, dm), are small.
Conclusions
If we made no calculation errors, a rotating ball pulls down a test mass on a prograde circular orbit, relative to a static ball. The force is equivalent to a gravitomagnetic moment
(2 / π - 1) J = -0.36 J.
This is different from the Kerr metric where the gravitomagnetic moment is 2 J.
The Kerr metric has the same gravitomagnetic moment 2 J for a test mass approaching radially. Our result is 1/2 J from August 10.
Who is right?
The Kerr metric is about masses moving relative to a test mass. If general relativity is not Lorentz covariant, it is bound to produce wrong results. The (asymptotic) Kerr metric most probably cannot be the correct metric for a rotating body.
Our results come from complicated calculations. There may be errors. Also, we have to check if our "linearity of solutions conjecture" is reasonable.
We do not know if the Kerr metric could still be good for strong gravity fields, like near a rotating black hole. We have to study that problem.
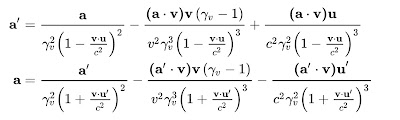


No comments:
Post a Comment