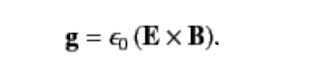Maxwell's equations describe charges in conducting objects?

In our September 18, 2024 blog post we had a negatively charged cylinder, and an electron e- moving close to it. We encountered a paradox: the electron did not get any acceleration along the cylinder, even though in the frame comoving with the electron e-, the cylinder creates a magnetic field B which should accelerate the electron in the x direction.

There is no acceleration of the electron in the x direction in the case of a charged electric insulator cylinder

      negatively charged insulator cylinder

      ========================== - 

                        ^ u                     W = F Δy

                        |

             -v <--- • e-      

                        |

                        v F Coulomb's force

              ^        ^

              |        |

              E       E'

    ^ y

    |

     ------> x  (laboratory frame)

Above, E is the electric field of the insulator cylinder and E' is the electric field of the electron. As the electron comes closer to the long cylinder, the electron does not acquire any momentum in the x direction.

The electron loses its kinetic energy as it comes closer to the cylinder. The inertia of the electron grows smaller. But the extra field energy in the field

       E  +  E',

relative to the plain fields E and E', grows as much as the electron loses its kinetic energy. The combination of the electron plus the extra energy in the field retains its inertia. The electron does not acquire any acceleration in the x direction.

The magnetic acceleration in the comoving frame of the electron: the Lorentz magnetic force formula fails for an electric insulator

        negatively charged insulator cylinder

        ========================= ---> v

             ○      ○      ○      ○    B    field lines point

                                                   out of the screen

                           ^  u

                           |

                          • e-

       ^ y

       |

        ------> x'  (comoving x')

In the comoving frame of the electron, the electron sees a magnetic field B which should accelerate it to the negative x' direction.

But this is inconsistent with the fact that the electron has no x acceleration in the laboratory frame.

What is going on? We proved that the Lorentz force formula is wrong for an electric insulator which is charged. The charges in the cylinder cannot move. It is an electric insulator.

A symmetric charged metal wire: the Lorentz magnetic force formula holds

                         midpoint         wire electrons

         ===========|===========  - 

                                  

                                 ^ u

                                 |

                     -v <---- • e- test electron

            |    |    |    |    |    |    |   E''

        ^ y

        |

         -----> x (laboratory frame)

If the charged cylinder is a metal wire, then conducting electrons can freely move inside it. Let the test electron be close to the wire, at the midpoint of the wire. The test electron repels the electrons in the metal. The combined electric field E'' of the system will be roughly constant far away. There is no stronger field at the location of the electron.

Now the electric field does not increase the inertia of the electron in the x direction. The inertia of the electron decreases as it approaches the charged wire. The electron accelerates to the left.

We see that the Lorentz force formula about B holds if the charged cylinder is an electric conductor. The Lorentz force takes into account both Coulomb's force and the backreaction of the electrons in the wire.

If the electron is not approaching the wire at the midpoint, then the situation is more complicated since the extra field energy is stored, on the average, at the midpoint. What happens then?

A single electron inside an electron gas cloud: the inertia is a constant me?

Let us look at the electron gas inside a block of metal. The thermal velocity of electrons is roughly 100 km/s.

If we move one electron e- along a long wire at a speed v, then to keep the field approximately constant, it has to be compensated for by moving a cloud of electron gas of N electrons to the opposite direction at the speed

       v / N.

There N is on the order of 10²³. The energy needed for the movement is

       ~  1/2 N me v² / N²

       =  1/2 me v²  *  1 / N,

where me is the rest mass of the electron.

We conclude that the inertia of the single electron e- does not grow appreciably from the effect on the electron gas. 

The conclusion: when an electron e- is very close to a metal wire, the "evening out" of the electric field done by repulsed electrons in the wire does not increase the inertia of the electron.

Ultimately, this effect should be measured, since it is a quantum mechanical process, and surprises can occur. An Internet search only returns one experiment where the inertia seemed to change. Apparently, in most cases the inertia change is negligible.

Also, the effect of the electrons in the gas moving at 100 km/s should be studied. The hypothetical electron which we "move", actually moves already at 100 km/s. The other electrons, which it repels, move at 100 km/s, too.

The electric influence of an electron close to a wire: a deficit of electrons worth e+

If we add a single new electron e- into an electron cloud, e- "makes room" for itself by repelling the amount e- of charge around it. There is a deficit of charge equivalent to e+ close to the electron.

                  deficit of electrons

                +       +    + + +    +       +

         ============|============  wire

                           midpoint                     length L

                                   • e-

What about a metal wire and a single electron e- close to it? Let us assume that the wire is very long and the electron e- is at the midpoint.

There is an excess of electrons now at the ends of the wire. Does the excess have any effect? The excess probably is ~ 1/2 e-. The charge density of the excess is

       ~  e- / L.

The electric field of the excess close to the center of the wire is negligible if L is very long.

On the other hand, the deficit of electrons close to the center of the wire does have a significant effect on the electric field close to the center.

Conjecture. The electron e- repels the electrons in a long wire in such a way that the deficit of electrons close to e- is equivalent to e+.

If the electron e- moves along the wire, it carries a fuzzy "positron e+" along with itself inside the wire.

An electron moving along a negatively charged metal wire: a more detailed analysis

      

                   deficit of electrons

                               "e+"

           v <---    +  + +++ +  +

             ======================  -  wire

                                                     negative charge

                                 ^ u    R = distance(e-, wire)

                                 | 

                       v <--- • e-

           |      |      |      |      |      |     E

       ^ y

       |

        ------> x

The "electric influence" of the electron e- repels electrons in the wire. A "positron e+" travels along with the electron.

The velocity component u takes the electron closer to the wire, and the velocity component u slows down. The inertia of the electron e- is reduced. But how does the inertia of the field, or the electrons in the wire, behave?

The combined electric field E of the wire and the electron e- at distances r > R from the wire has the lowest energy if E is approximately uniform. The field strength

       ~  1 / r

and the energy density

       ~  1 / r².

The circumference at a distance r from the wire is ~ r. Thus the total field energy is the integral of

       ~ 1 / r²  *  r  =  1 / r,

which diverges.

The field E is the sum of the field of the electron e-, the "positron e+", and a uniform charge density in the wire.

Most of the "interaction energy" of these fields is at distances r > R?

        ====================

                      deficit of

                   field energy        E

                  v <--- • e-

In the diagram we have marked the volume where the field E has less energy than it would have if the electron e- were not present. Does this "bubble"add much to the inertia of the electron e-?

As the electron moves to the left, field energy must flow to the right, so that the bubble moves with the electron. Does this energy flow possess much kinetic energy?

It is the Poynting vector

       1 / μ₀  *  E × B

which describes the energy flow. The flow takes energy from the left to the right along quite a straight path. Is there a lot of kinetic energy in this flow? Can we "grab" the flow?

The kinetic energy of flowing liquid

Suppose that we have a metal object M submerged into a water pool. The mass M of the object adds inertia to the object. The water in the pool starts to move if we move M. How much inertia does water add to M?

This is a complicated question.

In the electron gas cloud section above, we simply guessed that the extra inertia is negligible. The total kinetic energy of the system gives us a hunch of what the inertia might be, because

        1/2 M' v²

is the energy, where M' is the inertia of the object and v is its velocity.

If M causes a very large mass of water to flow very slowly, then the kinetic energy of that very large mass is negligible. If M is streamlined, the flow of water around it may have very little kinetic energy?

Then we can produce a significant momentum into the liquid, even though we only consume very little energy. How is that possible?

                   m     m

                 ■■|■■

                 ■■|■■

                       |

                       |

                       |  --> 

                   lever

The streamlined object may act like a "lever" which gives two large masses m a significant momentum, even though the energy spent is very little. In the lever configuration, there will be momentum both to the left and to the right.

The bubble of a lower field energy density has a constant effect on the inertia of the electron e-?

In the diagram in a preceding section, the electron drags along with it a bubble of a lower field energy density.

Can we harvest energy from the movement of the bubble, and harvest it separately from the movement of the electron?

We can "grab" the bubble at least through gravitation. The bubble is equivalent to a block of negative mass moving superposed to a constant density mass distribution. The flowing liquid example proved that the energy associated with such a movement can be negligible.

       ----> x       ================= - wire

      |                      ^

      v   r                 |  E  bubble

                                         |  E'

                                         v 

                                         • e-   

                                           R = distance(e-, wire)

Let us calculate how much energy is missing from the bubble in the case where there is an electron close to a negatively charged wire.

The field of the wire is

       -E₀ / r.

The missing energy density is

       ~ E E'

in the bubble. Close to the electron,

       E' ~ 1 / (R - r)²,

and E is roughly constant. The integration volume is ~ (R - r)² dr. The integral is

       ~ R - r.

Close to the wire, E ~ 1 / r, E' is roughly constant, and the integration volume is  ~ r dr. The integral is

       ~ r.

Let us calculate a very rough approximate value of the missing energy in the bubble. Let

       E  =  E₀ / r.

The electron is at a distance R. The electron field at the midpoint between the wire and the electron is 

       E'  =  1 / (4 π ε₀)  *  e- / (R - r)².

The missing energy density at the midpoint is

       ε₀ E E'  ≈  ε₀ E₀  *  2 / R 

                        * 1 / (4 π ε₀)  *  e-  *  4 / R²

                    =  2 / π  *  E₀ e- / R³.

The integration volume at the midpoint is something like

      1/4 R² dr.

The value of r varies 0 ... R. We conclude that the missing energy in the bubble is on the order of

       1 / (2 π)  *  E₀

electron volts. This can be compared to the mass of the electron, 511 keV.

In a typical experiment with a charged wire, the field strength at the distance of 1 meter might be at most 100 kV/m. If it affects the inertia of the electron, the effect is somehing like 15 keV, or 3%. The effect does not depend on the distance of the electron. Thus, the effect does not appear as a magnetic effect when the electron approaches the wire.

Conjecture 1. The bubble of missing lower field energy does not have much effect on magnetism.

The electric field at distances larger than R from the wire is roughly uniform, and does not add much inertia to the electron if it moves along the wire.

Conjecture 2. The inertia of the electron in a parallel movement with the wire does not depend appreciably with its distance R from the wire.

If the electron e- approaches the wire at a velocity u, it loses kinetic energy in its velocity component u. Conjecture 2 implies that its inertia is less as it comes closer. But the momentum is constant parallel to the wire. The electron e- accelerates in the direction parallel to the wire. This is seen as a magnetic "force".

Conjecture 3. An electron approaching a charged wire feels a magnetic "force" which is described by Maxwell's equations.

Poincaré stresses

Do Poincaré stresses have any signicance in the case of the charged electric insulator or a wire?

https://en.wikipedia.org/wiki/Maxwell_stress_tensor

Poincaré stresses counteract the pressure components of the Maxwell stress tensor of the field. In many cases, Poincaré stresses cancel the effects of pressures on the momentum of the system.

Our analyses in the preceding sections have ignored pressures altogether. We have only looked at energy flows. We can justify our choice by claiming that Poincaré stresses cancel all effects of pressures.

But this should be studied in more detail.

Oppositely charged cylinders which are electric insulators: the Lorentz magnetic force formula holds

In the previous sections we studied the magnetic "force" felt by an electron approaching a charged metal wire. The "force" in that case did not change the momentum of the electron, and, therefore, is not a true force. The acceleration happened because the inertia of the electron decreased.

Normally, a magnetic field is produced by an uncharged wire inside which there is a flow of electrons. Let us first treat a simpler case where the electric current is produced by a moving electric insulator. Then there is no electric influence on the charges in the insulator.

                       charged electric

                       insulator cylinders

             v <---  ---------------------------- +  protons

                       ==============  -   electrons

             v <---  ---------------------------- +  protons 

                        ○       ○       ○       ○    B

             attraction

                                ^  F

                                |            |

                                             v  F'

                                                     repulsion

                                     ^ u

                                     |

                           v <--- • e-

    ----> x

The outer cylinder is positively charged and is comoving with the electron e-. The inner cylinder is negatively charged and is static. The charges cancel each other out, so that the electric field is zero outside the cylinders. The magnetic field B is non-zero.

The static positive charge attracts the electron (the force F). The moving negative charge repulses (the force F').

In our September 18, 2024 blog post we were able to derive magnetism by assuming that the energy given to e- by F is "moving at a velocity v" to the left, and the energy taken by F' is "static".

Let us analyze this from the aspect of fields.

                              ^  W' energy packet

                              |

                               

                              ^ u

                              |

                    v <--- • e-

  

                           <- p' surplus momentum

      ----> x

      

In the first section of this blog post, the electron e- loses some of its "u-kinetic" energy

       1/2 me u²

to Coulomb's force. Let us denote this energy packet by W'. The packet does not "move" in the x direction. The electron would retain the x momentum in the u-kinetic energy; let us denote it by

       p'  =  W' / c²  *  v.

But the electron e- has to give p' to the extra field energy in the combined field of the cylinder and e-, and must drag this energy along with itself.

Let us then add the positively charged cylinder to the configuration. One may imagine that the energy packet W' now does not come from the u-kinetic energy of e-, but it comes from the attractive force between e- and the positive cylinder. The packet travels at the velocity v to the left. The momentum p' is now held by e-, and a "magnetic force" accelerates e- to the left.

Is this explanation plausible? Why the surplus momentum p' is not absorbed by the cylinders? Why is it held by the electron e-?

Conclusions

Let us close this long blog post. We will treat later the case where an electron approaches a moving positively charged cylinder.

We would need empirical measurements of the electron behavior close to moving charged insulators. It is difficult to determine the correct model using pure reasoning alone.

Poynting vector in a coaxial system

Let us look at the problem which we recognized in the previous blog post.

       ----------------------------- -  outer cylinder wall

             |      |      |   E

       ----------------------------- +  cylinder wall

  

       ----------------------------- +  cylinder wall

             |      |      |   E

       ------------------------------ -

                   --->  v

       ----> x

Let us consider a coaxial configuration where the electric field is nicely isolated between the cylinder walls.

The coaxial system moves to the right at the speed v. There is a magnetic field

       B  =  v / c²  * E.

The Poynting vector has the value

       ε₀ c² E  ×  B

  

       =  ε₀ E²  *  v.

A half of the value comes from shipping the energy of the field. The other half comes from shipping the x pressure of the field.

The Poincaré stresses which keep the cylinders from exploding cancel the pressure part of the momentum. The Poincaré stresses correspond to a negative pressure which cancels the positive x pressure in the field E.

                       ^  E'

                       |

                --------------  +      rod

                       |

                       v

Let us then add a static positively charged rod at the center of the cylinder. The field

       E  +  E'

is larger at the location of the rod. The Poynting vector to the right increases in value by

       ε₀ c² E'  ×  B

       =  ε₀ E × E'.

But there is no extra shipping of field energy or pressure in the x direction. How is it possible that the Poynting vector increases?

The answer: as elementary charges in the positively charged cylinder come close to the positively charged rod, they lose kinetic energy to the potential of the field of the rod. The charges the kinetic energy back when they recede from the rod. This is the origin of the energy flow in the field.

Conclusions

There is no paradox in this. We simply forgot to take into account the kinetic energy of the charges which create the magnetic field.

Now that we understand the energy flow in this case, let us return back to the Biot-Savart law.

Biot-Savart derived from Coulomb's force

UPDATE September 23, 2024: Electromagnetism is not "linear" if we take into account the field energy. If electric fields E₁ = -E₂, then the energy density of the sum field E₁ + E₂ is zero, but each individual field has a non-zero energy density. Keeping this in mind resolves many apparent paradoxes.

If an electron e- is close to a conducting object, like a metal wire, that causes a backreaction in the distribution of electrons in the metal. This will significantly affect the inertia which the electron e- feels. In the "cylinder of electrons" in the diagram below we ignored the backreaction. The strong electric field

       Eelectr  +  Ee-

is "diluted" over the entire length of the conducting metal wire. It does not add to the inertia of the electron.

It looks like that Maxwell's equations describe the electromagnetism of charged metal objects. The rules are different for charged electric insulators!

----

Let us try the derivation of the Biot-Savart law once again. This time we try to take into account the momentum of the field, and all other factors.

https://www.feynmanlectures.caltech.edu/II_13.html

The Feynman Lectures on Physics (1964) treats the case where a test charge q moves parallel to to a current-carrying wire. A more difficult case is when q directly approaches the wire.

A wire as two overlapping cylinders of charge: a simple explanation of the magnetic force on an electron e- approaching the wire

Let us model a long wire as two uniformly charged cylinders. The protons form a positively charged cylinder which is static in the laboratory frame. The electrons form another cylinder which moves very slowly relative to the laboratory frame: the speed is of the order of micrometers per second.

                  wire with a current

                 ●●●●●●●●●●                protons

                 •••••••••••••••••  ---> v      electrons e-

                 ●●  ^   ●●●●●                protons

                    |   |  W

                    |   |          ^ u

                    |   |          |

                   v              • e-

                  W energy packet

    ^ y

    |

     ------> x

Let us use this simple model:

1.   As the electron e- approaches the wire, it receives an energy "packet" W from its Coulomb attraction to the protons. The packet W has a zero momentum in the x direction.

2.  The electron must give the energy packet W back to the electrons in the wire, because there is a Coulomb repulsion. This time W must comove with the electrons in the wire, to the right at the velocity v. The packet must contain a momentum

        p  =  W / c²  *  v

to the right.

3.  The electron is left with a momentum p to the left. This is the "magnetic" force which accelerates the electron to the left.

Let us next analyze this in detail, trying to make sense of the field energy and momentum.

A uniformly negatively charged static cylinder and an approaching electron e-

       =============== -  cylinder of electrons

                        ^  u                   W = F Δy

                        |

             -v <--- • e-      

                        |

                        v  F   Coulomb's force

              ^       ^

              |       |

            Eelectr  Ee-

    ^ y

    |

     ------> x

The cylinder consists of the electrons inside a wire. As the electron e- approaches the cylinder, it loses a kinetic energy W. There is no change in the x momentum of e-.

Coulomb's force describes the interaction between charges: we ignore the momentum in the electric field. Since e- loses kinetic energy, its inertia is diminished. The electron accelerates to the left. In the frame of the protons in the wire, this acceleration in interpreted as the magnetic force.

If we take into account the field, then the situation looks different. The extra energy W is now in the combined field

       Eelectr  +  Eq,

which is moving to the left. The momentum to the left of the electron e- and of the extra field energy W has grown. The interaction pushed this combined system to the left.

But now we face a dilemma: if the system acquired a momentum to the left, then the cylinder must have acquired a momentum to the right. The Lorentz force says that the cylinder did not acquire any momentum to the right. Is the Lorentz force formula incorrect, after all?

Conclusions

We are able to derive the magnetic force with a very simple model where we only take into account Coulomb's force, and ignore the electric field momentum.

But if we include the electric field momentum, then the Lorentz force formula seems to be broken. We will investigate this more in the next blog post.

Lorentz covariance of electromagnetism

In the summer of 2023 we suspected that Lorentz covariance does not work correctly in electromagnetism. Let us return to this question.

https://en.wikipedia.org/wiki/Lorentz_force

Moving charge Q and an approaching test charge q

                      Q ● ---> v

        

                                                    W = q E Δy

                          ^ u       ^ q E     Lorentz force

                          |           | 

                          • q        -----> q v × B

                         /

                         \

                         /    spring

                         |   F = -q E

                         v

        ^ y

        |

         ------> x

Let Q be positive and q negative. The charge Q creates an electric field E, and a magnetic field B which steers q to the right, according to the Lorentz force.

The spring and the force F on it cancels out the electric attraction q E between q and Q.

There is no retardation in the field of Q. If Q is to the y direction from q at the time t = 0, then the electric field E of Q points directly to the y direction at the time t = 0.

Switch to a comoving frame of Q

                              ● Q

                                                         W = q E Δy

                              ^ u        ^   q E   Lorentz force

                              |            |   

                   -v <--- • q

                             /

                             \

                             /  spring

                             |   F = -q E

                             v  

            ^ y'

            |

             -----> x'

The electric field E' points to the y' direction, and there is no magnetic field B. The momentum of q does not change with time.

The Lorentz force says that q does not have an acceleration in the x' direction in this case.

This seems to break Lorentz covariance. The problem is that the Lorentz force does not take into account the momentum held by the energy

       W  =  q E Δy,

which q receives from the field of Q. By Δy we denote the distance which q moves to the y direction.

In the first diagram, the energy W holds momentum to the positive x direction (and this also explains the magnetic field B: we do not really need to consider B at all).

Is the Poynting vector aware of the momentum in W?

Maybe the Lorentz force simply is an imprecise description of the electromagnetic action? Let us check if the action understands the momentum held by W.

Does the Poynting vector

        1 / μ₀  *  E  ×  B

understand that in the first diagram, the energy W flowing to q contains momentum to the positive x direction? And that in the second diagram, W does not contain momentum to the x direction?

The energy W flows further to the spring. We assume that in the first diagram, that flow does not contain x momentum. The momentum is retained by q.

Second diagram. The magnetic field of the negative charge q moving to the y direction makes the Poynting vector 1 / μ₀ * E × B to point toward q on both sides of q:

                             ● Q

                             |

                             |  E

                             v

                             ^  u

                             | 

                  -v <--- •  q

                B ×                 ○  B

            

                   --->            <---

                E × B            E × B

Above, × denotes a magnetic field B line produced by q coming up from the screen, and ○ is a field line going into the screen. We ignore the magnetic field associated with the -v velocity vector.

The Poynting vector 1 / μ₀ * E × B brings field energy to q. Is the diagram symmetric versus the energy flows, or does q receive more energy from the left, as q moves to the left at the speed v?

First diagram. 

                        

                         Q ● ---> v

                             |

                             |  E

                             v

                             ^  u

                             | 

                              •  q

                B ×                 ○  B 

            

                   --->            <---

                E × B            E × B

The first diagram looks more symmetric. The Poynting vector seems to bring the same energy flux from the left and from the right. But the charge q should accelerate to the right. There is something wrong.

Does the magnetic field of Q change this somehow?

Replace Q with a part of a wire with an electric current: analysis of the Poynting vector to q

Let us check if the Poynting vector handles a pure magnetic field correctly. We put an opposite static charge -Q close to Q, so that the electric field E of them is essentially zero at q. 

                        -Q ●

                         Q ● ---> v

                           

                    

                     

                             ^  u

                             | 

                              •  q

               Bq ×                 ○  Bq  

            

                   --->            <---

               E × Bq            E × Bq        E = 0

         ^ y

         |

          ------> x

The fields close to q are now:

1.   The electric field produced by Q and -Q is EQ = 0.

2.   The magnetic field BQ produced by Q is significant.

3.   The fields Eq and Bq produced by q are significant.

The Poynting vector Eq × Bq cannot bring any momentum to q. Only

       1 / μ₀  *  Eq × BQ 

might possibly bring momentum. But Eq is almost radial to q, and Eq × BQ is orthogonal to Eq. If q accelerates to the right, is the electric field deformed enough, so that the Poynting vector could give momentum to q?

https://farside.ph.utexas.edu/teaching/jk1/Electromagnetism/node11.html

(Richard Fitzpatrick, 2014)

Conservation of the electromagnetic 4-momentum is this formula:

The term j × B is the force which pushes q to the right, to the positive x direction. We are interested in the coordinate i = 1, which is the x coordinate.

Is -∂ (ε₀ E × B) /  ∂t then non-zero?

Make q very heavy and push it suddenly toward Q and -Q: momentum conservation works correctly

We suddenly push q to the positive y direction, so that it acquires a velocity u. The x coordinate of Q, -Q and q is the same after the push operation.

Can q somehow acquire momentum to the right, from the electromagnetic field? The speed of light is finite. The momentum must come from a close location to q.

                 -Q ●

                  Q ● ---> v

                      |

                      | line L of cylindrical symmetry

                      |

                      |

                      ^ u

                      |

                      •

                      q

      ^ y

      |

      ○ ----> x

     z points out

     of the screen

Let us assume that q is extremely heavy, so that its acceleration to the right is very small, even though it gets a lot of momentum to the right from the magnetic field BQ. Since q moves almost exactly to the positive y direction, then the fields Eq and Bq of q are almost exactly cylindrically symmetric relative to the line L which contains q and runs to parallel to the y axis.

Let us assume that the distance from q to Q and -Q is very large, and that Q and -Q are very close to each other.

Then the electric field EQ-Q of Q and -Q is almost exactly zero close to q. The magnetic field BQ of Q is almost exactly parallel to the z axis, and is almost exactly uniform.

https://farside.ph.utexas.edu/teaching/jk1/Electromagnetism/node11.html

The field momentum is

The field momentum close to q in Eq × Bq points to the y direction, on the average.

Let us study the field Eq of q at some distance r.

https://physics.weber.edu/schroeder/mrr/MRRtalk.html

Daniel V. Schroeder (1999) drew the electric field lines if a charge q is initially static, but is pushed and acquires a speed u upward. The diagram shows the field lines after a little while.

What is the vector Eq × BQ like?

Below q in the picture, that vector points to the left, and above q, the vector points to the right. As q moves up, the field will contain more momentum to the left. This may explain how q itself gains momentum to the right?

The Poynting vector does not bring any new energy to q, but the movement of q changes the amount of x momentum in the integrated Poynting vector.

If we stop the y movement of q, then Q and q absorb the x momentum stored in the field.

The electromagnetic momentum conservation probably works correctly in this case.

The Lorentz force does work correctly

Let us look again at the case where the electric attraction of Q is counteracted with a spring, rather than putting a charge -Q close to Q.

We may assume that the spring is attached to the laboratory table.

                              ● Q

                                                         W = q E Δy

                              ^ u        ^   q E   Lorentz force

                              |            |   

                   -v <--- • q

                             /

                             \

                             /  spring

                  -v <--- × attachment

                             |   F = -q E

                             v  

            ^ y'

            |

             -----> x'

In the moving frame, the spring moves to the left along with q. Now we see that the movement of q to the left will slow down as time passes. That is because q receives an energy packet W which is static relative to Q. But q has to pass W to the spring which is moving to the left. Then q has to give up some of its own momentum to the left. We conclude that q accelerates to the right, just as it should do.

Does the energy W which q gains in the field of Q have a zero momentum relative to Q?

                           ● Q

                           |  EQ

                           v   

                                                 W = F Δy

                                      ^ F

                           ^ u     |  Coulomb's force q EQ 

                           |

                -v <--- • q

       ^ y

       |

        ------> x

We still have to check if the energy packet W really is static relative to Q. Or does the velocity -v of q affect this?

If the Lorentz force formula, or Coulomb's force formula is correct, then q does not receive any momentum in the x direction. Then W really has a zero momentum relative to Q.

We can take as an axiom that Coulomb's force points exactly toward a static charge Q. If Q is accelerating, then this gets more complicated.

Conclusions

Classical electromagnetism fared well in this test of ours. Lorentz covariance and momentum conservation were worked ok.

We can take as an axiom that Coulomb's force points directly toward a static charge, and that it gives an energy packet W which is static relative to Q.

Then we can derive the Biot-Savart law for a wire segment. The derivation of Zile and Overduin (2014) can be corrected this way. We will write a new blog post about Biot-Savart. We will also look at the August 28, 2024 overlapping electric fields again, now that we understand 4-momentum conservation better.

Zile and Overduin: Biot-Savart law from special relativity and Coulomb's law

On December 17, 2023 we claimed that we can derive the Biot-Savart law from Coulomb's force and a few additional assumptions. But the assumptions were dubious. Daniel Zile and James Overduin in their 2014 paper touched the same problem.

The derivation by Zile and Overduin of Biot-Savart from Coulomb and special relativity

https://en.wikipedia.org/wiki/Biot%E2%80%93Savart_law

The Wikipedia article contains a link to the following paper:

https://www.researchgate.net/publication/261597268_Derivation_of_the_Biot-Savart_law_from_Coulomb's_law_and_implications_for_gravity

Daniel Zile and James Overduin (2014) derive Biot-Savart from Coulomb's force and a special relativistic transformation of forces in a moving frame. Their derivation uses a "mass transformation". The transformation seems to be the total energy of a moving point particle in another frame.

Their momentum transformation is the 4-momentum transformation of a particle to a new frame.

https://hepweb.ucsd.edu/ph110b/110b_notes/node54.html

(Jim Branson, 2012)

Above, β = v / c. The 4-momentum transformation of Zile and Overduin contains a typo in the following line:

where mu probably means E / c² in the notation of the authors. It should be

       v E / c².

The letter v is missing.

                   Q ●

                       ^  u

                       |

                       • ----> V

                      q

      ^  y

      |

       ------> x

Let us analyze what the authors calculate in the above simple configuration. Let Q be positive and q be negative. As q approaches Q, the particle q gains energy from the field of Q, and the velocity V slows down since the x momentum stays the same.

Let v = V at the time t = 0. We switch to a frame which moves at a velocity v to the right. In that frame, it appears that a force is accelerating q to the left because V is slowing down. We can interpret that in the moving frame, Q has a magnetic field B, and the Lorentz force

       q v  ×  B

is accelerating q to the left. This is the "force transformation" of Zile and Overduin.

This phenomenon is the inertia effect which we observed in our blog several years ago. It can explain B, starting from the Coulomb attraction between q and Q. Zile and Overduin made the same observation in 2014, as we made a few years later in this blog.

The error in the Zile and Overduin argument

In a wire carrying an electric current, the protons essentially cancel Coulomb's force which moving electrons exert on a test charge q near the wire.

The argument of Zile and Overduin rests on the fact that the total energy E of q increases (or decreases) as q approaches the wire. This does not happen.

How to correct the argument of Zile and Overduin?

We must take into account the momentum of the energy W which the test charge q gains in the field of Q.

Let q be a positron. As q approaches the electrons in a wire, it receives a "moving" packet of energy W in the field of the electrons. The packet contains momentum, besides energy.

The positron q must use the energy W when it climbs in the potential of the protons of the wire. But the positron cannot give up the momentum that it got in the packet W. The positron will steer to the direction where the electrons are moving.

Conclusions

Our proof of the Biot-Savart law on December 17, 2023 contained assumptions which are dubious. It is better to use the argument that the energy packet W which a test charge q receives in the field of a moving charge Q, also contains momentum. We will analyze this in a future blog post.

On August 28, 2024 we observed that the electromagnetic action seems to be ignorant of the kinetic energy of two overlapping electric fields. Our analysis of Biot-Savart above depends on the energy packet W possessing momentum. It is another subtle effect of overlapping fields. The electromagnetic action does handle it correctly by introducing the magnetic field B.

Electromagnetic lagrangian: correcting it with special relativity

Our August 28, 2024 post suggests that the electromagnetic lagrangian (or action) does not understand the kinetic energy of two overlapping electric fields E + E'. This means that Maxwell's equations do not understand it either.

Is there a generic way in which we can make a lagrangian to respect special relativity?

Moving elastic energy

Let us look at an elastic solid block. How does a physical model understand that moving elastic energy should possess kinetic energy and momentum?

    =====================  elastic block

    =====================  

    wedge  /\   ---> v               ● obstacle

                  ^    moving wedge

                  |    presses the block

                  F

Let us have an elastic block which a wedge presses upward with a force, causing a distortion which contains elastic energy. The block is very lightweight, so that the kinetic energy of its atoms is negligible.

If the wedge moves at a velocity v, there should be momentum associated with the moving elastic energy. Otherwise, the center of mass of an isolated system could move.

Since there is momentum, the wedge can bump into an obstacle, giving it momentum and kinetic energy. This proves that the elastic energy must contain kinetic energy, too.

How do we model this system in special relativity?

https://en.wikipedia.org/wiki/Strain_energy

Usually, the kinetic energy of elastic energy is ignored, and a lagrangian density is written simply for the elastic energy content:

       L  =  -1/2 E ε²,

where E is Young's modulus and ε is the strain. The elastic energy is so small that we do not need to care about its momentum and kinetic energy.

Writing truly special relativistic lagrangians

Is there some simple way to write the kinetic energy into the lagrangian density? Let us look at the stress-energy tensor of the elastic energy. Maybe we should treat potential energy just like a massive particle is treated?

https://en.wikipedia.org/wiki/Four-momentum

In quantum mechanics, any particle is an excitation of a field. It is natural to treat elastic energy in the same way as a massive particle?

https://en.wikipedia.org/wiki/Relativistic_Lagrangian_mechanics

The Wikipedia article contains a lagrangian for a charged particle q in an electromagnetic field (φ, A), but it ignores the kinetic energy of the potential energy of the particle q.

Conclusions

A correct special relativistic lagrangian for electromagnetism can be quite complicated to write. In many cases, the lagrangian found in literature is precise enough.

If an electron is under a large potential from a charged insulator, then its potential energy does have major effects. Our solution of the Klein paradox on October 31, 2018 relies on the extra inertia which an electron acquires at a steep potential wall.

Special relativity and moving pressure

In our August 28, 2024 blog post we were confused about if the horizontal Maxwell stress tensor pressure in the sum field E + E' "moves" with the field E', along with the moving rod.

What does a "moving pressure" mean in special relativity?

In the Lorentz transformation of the stress-energy tensor, a positive pressure to the direction of the movement shows up as a positive energy density and as positive momentum. For negative pressure, the signs are flipped.

A moving pressure is something where the action and the reaction are simultaneous in a moving frame

                positive pressure

                       <---------->

                M ●                 ● M

                       >----------<

               negative pressure

 

                             ---> v

If the system is static, but moving, then positive and negative pressures cancel each other out, and we can ignore pressures if we are concerned with the entire system.

If we remove the negative pressure, what happens?

The positive pressure shows up as momentum to the right in the stress-energy tensor, and also as energy. Does this make sense?

Simultaneousness is different in the laboratory frame relative to the moving frame. Let there be a short positive "pressure pulse" in the moving frame. An observer in the laboratory frame sees the mass M on the left to accelerate to the left before he sees the mass M on the right to accelerate. The momentum and the energy in the pressure is "buffered", and will eventually be seen in M on the right.

We conclude that in this case, momentum and energy contained in pressure makes a lot of sense.

The force field between the two M is "moving" along with them. The action and the reaction are simultaneous in the moving frame.

A static charge Q and a moving charge Q

          ●                   ● ---> v  

          Q                  Q

Does the electric field in this case "buffer" momentum, if looked at in the laboratory frame? Yes, of course. In the frame moving at the velocity v / 2 to the right there is no buffering, because of symmetry. In other frames, there is buffering.

Momentum conservation would be broken if we would not assign some momentum to the field.

          ● ---> v            ●

          Q                     Q

In the configuration above, we, similarly, see that the field does not buffer any momentum in a frame which moves at the speed v / 2 to the right.

But the field does buffer momentum to the right if looked at in the laboratory frame.

In this specific case, the "pressure" between the various Q is "moving" to the right at the speed v / 2.

Adding Poincaré stresses

        =========================   rigid rod

           ●        ● ---> v        -F <---- ●  ----> F

           Q       Q                              Q

                                                 

Let us imagine that the leftmost and the rightmost Q are attached to a rigid rod. The rod provides the Poincaré stresses for them.

If we want to keep the those two Q exactly static, we have to imitate the forces F exerted by the middle Q, but flip the sign of the force.

We could hypothetically create such forces by adding a new interaction, such that the middle Q pulls the other two Q. The moving pressure for the new interaction is the same as for the electric repulsion, but the sign flipped. In this case we can claim that the negative Poincaré stress pressure exactly cancels out the positive pressure.

Conjecture. The Poincaré stresses which are required to cancel out the pressure from an electric field, are "moving" pressures, and their contribution cancels out the momentum and the energy contribution of the pressure of the electric field.

Conclusions

We now understand what is the role of a "moving" pressure in special relativity. It has to contribute to the momentum and the energy in the stress-energy tensor, to preserve conservation of momentum and energy. Otherwise, the difference of simultaneousness in moving frames would break conservation laws.

Field theories cannot capture everything about interactions?

Consider a group of people. These people have complex interactions. Much of the interaction can be described as "messages" from one person to another.

Can we describe the interaction between people as a "field"? That is unlikely. Much of the communication is private between two persons.

Public communication, which can be accessed by anybody, is more likely to form a "field". People receive impulses from the public communication field, and give their own feedback to the field.

A field theory describes a very simple type of interaction between agents. The simplicity makes it easy to make predictions. 

https://www.goodreads.com/quotes/10558974-richard-feynman-the-great-physicist-once-said-imagine-how-much

On the Internet there is a quote (probably erroneously) attributed to Richard Feynman:

“Imagine how much harder physics would be if electrons had feelings.”

https://www.cnbctv18.com/views/when-issac-newton-lost-a-fortune-in-the-stock-market-1256171.htm

A similar quote is (probably falsely) attributed to Isaac Newton:

"I can calculate the movement of the stars, but not the madness of men."

In this blog we have suspected that interactions between particles are too complicated to be precisely described with a field theory. A "field" is lacking information which we would need to describe physical phenomena. Similarly, there might not exist a lagrangian or an action which describes how particles behave.

We will continue our efforts to find a logical description for gravity and electromagnetism. We do not know yet if a field theory is adequate, or if there exists a lagrangian.

Quantum field theory is a "message-passing" theory where particles exchange "virtual" particles. A message-passing formalism might solve some of the problems that we have encountered.

Negative energy of an electron in a potential

In a laboratory, one can create potential differences of up to 32 megavolts. Let us imagine that we put an electron to an electric potential which makes it potential energy much less than -511 keV. How does such a strange electron behave?

An electron inside a charged metal sphere, or close to it

                  |

              _____

           /            \   metal sphere

     --- |   • e-        |-----

           \_______/

                  |  

                     E symmetric electric field

If the electron is put inside a metal sphere, it will influence (polarize) charges into the sphere, such that its field will be centered at the center of the sphere. Then the inertia of the electron is only 511 keV inside the sphere. This may explain why experimenters have not noticed that the inertia of the electron depends on the potential. They should create the potential with static charges and remove all metal from the experiment setup.

Moving the electron tangentially close to the surface of the sphere induces an electric current to the surface, which creates a magnetic field B. This does increase the inertia, but then we interpret that the inertia is in the current.

An electron approaching a charged metal sphere

What about an electron approaching a charged metal sphere? 

                                  

        e- ●             |               ● e+ "mirror image"

                     metal wall

Close to a flat metal wall, the field of an electron, and the charges it displaced in the metal, will appear as a dipole field, because the field has to be normal at the wall. There is a "mirror image positron" on the other side of the wall.

If the metal wall is replaced by a metal sphere, then the charge which the electron repelled cannot escape to infinity. The repelled negative charge goes to the other side of the sphere.

We guess that the field of the electron and the metal will look like that the metal sphere "stole" some charge from the electron and put it to the center of the sphere.

The inertia of the electron in a tangential motion relative to the sphere may be unchanged, 511 keV?

     

         e- ● --> v        |     ×     |

                                   sphere

Let the electron approach a negatively charged metal sphere. Then there is energy shipping to the field of the sphere from the kinetic energy of the electron. This energy is shipped, on the average, to the center of the sphere? Does the energy shipping increase the inertia of the electron if it moves radially?

The kinetic energy is at the electron. The field which gains energy is centered on the center of the sphere. The energy flow is visible in the Poynting vector.

Can one "grab" the energy flow? Then the flow would contain some momentum which is visible to outside observers. The energy flow shows up in the gravity field as the mass-energy of the system moving to the right. It is plausible that one can "grab" it, and it does increase the inertia of the approaching electron. It may be possible to measure this effect.

Experimenters may have thought that the changes in the inertia are due to the kinetic energy of the electron, or due to currents in the metal. The changing inertia may have escaped their detection.

Conjecture. A charge q in a slow radial motion toward a charged metal sphere shows a larger inertia than in empty space.

Negative energy in an electron

If the metal sphere has a large positive charge, then an electron inside it has a negative total energy.

Our reasoning above says that the electron will still appear to have a positive inertia of 511 keV, because the field of the electron & the metal outside the sphere does not move if we move the electron inside.

This may explain why the spectrum of an atom does not change with the electric potential. If the potential is created with metal, the electric influence in the metal screens the change in the field?

A nucleus and an atom are not insulators?

Quarks move around inside a proton or a neutron, and protons and neutrons move around in a nucleus.

Electrons move around in the electron cloud of an atom. This suggests that the a nucleus or an atom may behave quite like metal, and does not increase the inertia of an electron in the electron cloud.

If we change the inertia of the electron in the x direction, but not in y or z, does that affect the spectrum of an atom? Yes

Above we speculate that the energy shipping close to a charged metal sphere changes the inertia of the electron in the radial direction. What would happen to the spectrum?

  

                      ● proton

                 e-  • --> v

There would be no change if the "spatial metric" would be squeezed to the radial direction. But it is unlikely that the electric field if the proton is squeezed. Thus, in the case of an atom, the inertia of an electron cannot be different to the radial direction.

The paradox of the energy flow of an electron circling a nucleus and a charge Q some distance away

                                         --> E' field of electron

               <-----  E field of Q

                ●   • e-                           ● Q charged

           proton                                         sphere

                                 1 meter

Let us put the atom at a distance 1 meter from a charged metal sphere Q. The electron makes some 10¹⁶ rounds around the nucleus in a second, in which time light moves about 10⁻⁸ meters.

Any energy shipping in the field E + E' can only come over a very short distance.

For very slowly moving charges q outside the sphere, the Poynting vector ships the energy from far away: from roughly the distance of one meter.

How does the energy flow in the combined field E + E' when the electron does its loop around the proton?

Is there an electromagnetic wave which moves energy back and forth in the field E?

The wave generated by the electron has the radial field E' essentially zero at large distances because there are no longitudinal electromagnetic waves.

What is the inertia of the electron like?

Let us imagine an analogous system in newtonian mechanics.

         m     spring       M

           • /\/\/\/\/\/\/\/\ ●  

        <-->

If we accelerate the small mass m very slowly we will observe that its inertia is m + M, because of the spring.

But if we move m back and forth very rapidly, its inertia appears as m.

This may explain the spectrum of atoms close to a charge Q. Since Q is much farther than 10⁻⁸ meters, the electron will not see much extra inertia to the radial direction, or to any direction. The combined field E + E' of the electron and Q will not have time to react to the rapid movements of the electron.

However, we have a quantum mechanical problem here. Let us have a hydrogen atom in the ground state. We bring it close to a charge Q. If the combined field of Q and the electron would "vibrate", that would steal energy from the atom. One cannot steal energy. This shows that there cannot be any visibly changing field of the electron outside the atom.

We have two solutions for the paradox:

1.   for any rapidly oscillating electron, the far field with an external charge Q does not have time to adjust to the movements of the electron: Q cannot give much extra inertia to the electron;

2.   an atom in a ground state, or in an almost stationary excited state, cannot possess an electric field which oscillates visibly outside the atom: the combined field of Q and the electron cannot give much inertia to the electron.

An electron close to a charge in an insulator

A macroscopic, charged insulator contains a huge number of electrons. Very little polarization makes the insulator to mimic the influence effects that an electron has on a metal object.

If we have a macroscopic charge Q, its electric field cannot exist inside metal, but can exist inside an insulator.

Can even very weak electric fields, like that of an electron, exist inside an insulator? Let us check the literature.

https://en.wikipedia.org/wiki/Insulator_(electricity)

Wikipedia states that an insulator always contains a small number of mobile charge carriers. If we add a significant charge Q into an insulator, do mobile charge carriers still exist?

The literature says that static electric charges are typically in the nanocoulomb range. They do create significant electric potentials. Then mobile charge carriers presumably decide their location based on the potential. If we have an individual electron close to the insulator, it probably cannot affect much the location of charge carrierd.

We conclude that a charged insulator does not behave like metal when we move an electron close to it. It might be possible to measure the inertia change of an electron in the electric field of the insulator.

The negative energy of the electron close to a nucleus, or close to a charged insulator

What would happen if we have an electron at a potential where its total energy is negative, i.e., if its potential energy is < -511 keV?

The rod inside a cylinder example of our August 28, 2024 blog post is a way to study this question.

                  |  |  |  |                |  |  |   E

            +  -----------------------------------  cylinder

                       rod   - --------   ---> v

            +  -----------------------------------  cylinder

                  |  |  |  |                |  |  |   E

                                   -m "negative mass"

                                              ● M

The cylinder is attached to a table at a laboratory. The rod makes a "hole" into the energy density

       1/2 ε₀ E²

of the electric field of the cylinder. Is it possible to "grab" the momentum if the hole moves?

https://en.wikipedia.org/wiki/Torus

                   

Let us make the cylinder into a torus by attaching the ends of the cylinder. Let the rod be long. As the rod moves inside the torus, there probably is angular momentum present in the field E of the torus. One can probably "grab" the angular momentum through the gravity which the field E creates.

Let us put a mass M close to the torus. Let it grab some angular momentum from the rotating energy in the field E. M gains momentum and kinetic energy that way. This implies that the rotation in the field E must have contained kinetic energy.

Our reasoning suggests that, even though the total energy of the rod is negative, as it is located in a very low potential, the rod still has a positive inertia, and a moving rod stores kinetic energy into the rotating field E.

It is like moving a submerged balloon in a swimming pool. The water around the balloon gives inertia to the balloon.

Conclusions

Our analysis assumed that charges move relatively slowly. If an electron is close to a charged metal object, like inside a charged metal ball, the inertia of the electron may not increase at all, since the polarization of charge in metal screens changes in the combined field of the metal object and the electron. This may be the reason why experimenters have not noticed any change in the inertia of the electron.

Quantum phenomena probably screen the change of the inertia of an electron inside an atom.

For very rapid oscillations of an electron, the far field of the electron does not have time to adjust. This screens changes in the inertia in certain cases.

A proton, or a nucleus, may behave somewhat like metal, since there are moving charges in the quarks inside. This may explain why an electron inside a hydrogen atom seems to have a constant inertia.

If an electron is close to a charged electric insulator, we should see a change in the inertia of the electron, since substantial energy in the combined field of the insulator and the electron move around.

Experimenters should measure the inertia of an electron close to a charged insulator. If the inertia does not differ from a free electron, then the existence of the electric "field" as an entity comes into question.