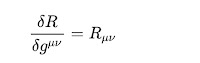UPDATE May 21, 2024: We found some of the problems. See the update of the May 10, 2024 post.
----
In the previous blog posts, we were not able to get any calculation right using the Einstein-Hilbert action. What is the problem?
The nonexistence of solutions of the Einstein equations for shear suggests that a lagrangian for the Einstein equations does not exist at all
Let us reconsider the cylinder with a shear. The lagrangian for a static solution is the "potential energy" of the system. We have to minimize the potential energy, in order to find the minimum of the action integral.
The Einstein field equations in this case must follow from the formula of the potential energy, through variational calculus.
Then the Einstein field equations would be satisfied in the state with the minimal potential energy.
On April 22, 24, and 26, 2024 we calculated various examples where the Einstein field equations do not seem to have an "approximate" solution for a cylinder with a shear. We can explain the nonexistence of a solution, if either:
1. the potential energy in the supposed lagrangian has no minimum value,
or
2. there does not exist a lagrangian at all.
Is it possible that we have a lagrangian where the cylinder with a shear does not have a state which has the lowest potential energy in gravity plus other fields? How could that happen?
1. The cylinder collapses into a singularity? That does not occur in nature. Cylinders on Earth do not collapse!
2. The cylinder approaches a minimum potential energy, but can never attain it? That would be strange. If we have a sequence of states of the cylinder, and the potential energy decreases in that sequence, then we would expect that there is a "limit" state which has the lowest potential energy.
It could happen that a sequence has no limit state. But that would be surprising. We have observed in nature that systems with potential energy in them, tend to approach an equilibrium state, and that equilibrium state is the "limit" of the successive states of the system.
An example: a complex oscillating mechanical system. It constantly loses energy in friction, and approaches a state where the potential energy is at a minimum. The minimum is the limit of the successive states of the system.
Our reasoning actually proves that the Einstein field equations are an incorrect theory of nature in the case of a cylinder with a shear. We have observed in nature that there does exist a minimum potential energy state for them. That state would satisfy the correct theory of gravity. But it does not satisfy the Einstein field equations. They are an incorrect theory of gravity.
The lagrangian of newtonian gravity, or static electric fields
Above, we have the lagrangian of newtonian gravity. There, Φ is the potential, and ρ is the mass density.
The lagrangian L(x, t) calculates the negative potential energy of the system. That is, the lagrangian is of the familiar type
T - V,
where T is the kinetic energy and V is the potential energy.
We have to maximize the integral of L(x, t), in order to find the equilibrium state. Then the potential energy is at the minimum.
Let us have a mass M sitting in space. We start from a flat zero potential Φ. If we make Φ(x, t) negative at the location of M, we can increase the integral of the last term:
ρ(x, t) Φ(x, t),
i.e., increase the value of the action integral.
But then the integral of the first term,
-( ∇Φ(x, t) )²
grows smaller. The integral over the whole lagrangian density attains the minimum when the potential Φ is the familiar newtonian gravity potential.
Let us analyze the logic of optimizing the integral to the maximum value:
1. we reduce the energy of the mass M by dropping it into a lower gravity potential Φ; the last term in L(x, t) describes this fall into a lower potential;
2. the price we have to pay is that the "energy of the field", ( ∇Φ(x, t) )², increases. At some point, it no longer pays to drop M any lower.
A rubber sheet model of gravity describes the optimization process qualitatively. The potential Φ is the height of the surface of the rubber sheet. The energy of the field, ( ∇Φ(x, t) )², is the elastic energy of the rubber.
If we think of static electric fields, then Φ is the electric potential, ∇Φ is the electric field strength, and (∇Φ)² is the energy of the electric field. An electric charge distribution Q digs a potential pit for itself, to get itself into a lower electric potential. Actually, if the field outside looks like the field of a positive charge, then Q is really a negative charge!
Can we describe the energy of a field through a "curvature" or charge density? No
In the Einstein-Hilbert action, the energy of the field is given in a different form: the scalar curvature R of the metric g. Can that idea work?
Something similar in newtonian gravity or electromagnetism would be the second derivative of the potential,
∇²Φ.
In electromagnetism, ∇²Φ is the charge density. Similarly, the Ricci scalar R gives the mass density ρ, in the absence of pressure or shear.
If we have a uniform spherical charge density Q, then we certainly can find some formula which, in terms of
∇²Φ, gives the total energy of the electric field around Q.
But is that possible for more complex charge distributions?
If the Einstein-Hilbert action would work for gravity with weak fields, then we could use it to determine the newtonian gravity potential (from g₀₀), and we would then have an "alternative" lagrangian for static electric fields, where the lagrangian density is in terms of charge density and the electric potential. Is it possible to form such a lagrangian?
The precise problem: can we determine the energy of an electric field "directly" from the charge density, without going indirectly through the calculation of the electric field E, and integrating E²?
It is not possible to determine the energy of the electric field from the charge density alone. Consider a thin spherical shell of charge. We keep the total charge Q constant and slowly shrink the radius in the shell. The energy of the electric field outside the shell grows. But we can let the thickness of the shell grow in such a way that the density of the charge per volume stays constant in the shell.
It does not help either, if we are allowed to calculate a "boundary term" from the electric field at some large radial distance. The electric field far away stays constant. It does not tell us how much the energy of the electric field is at small radial distances.
How can then the Einstein-Hilbert action work at all? The Ricci scalar R is essentially linear in the mass density ρ.
If there is no error in this reasoning, it explains why all our calculations with variations last week led to an error. The Einstein-Hilbert action does not contain the lagrangian for gravity.
The Einstein field equations lead to the Schwarzschild metric, and do describe gravity fairly well. But the Einstein-Hilbert action is a completely unrelated formula which does not describe gravity.
Formulating the correct lagrangian for static or dynamic solutions of the Einstein field equations
If the Einstein-Hilbert action is totally wrong for the Einstein field equations in a static setting, we would like to formulate one which works for static mass configurations.
Our November 5, 2023 result suggests that the Einstein field equations are not satisfied if there is a change in pressure, i.e., in a dynamic setting. Our April 22, 24, and 26, 2024 results suggest that there is no static solution if there is shear inside a cylinder.
It is still possible that a lagrangian exists for a pure mass distribution, both in a static and dynamic setting.
The first candidate, of course, is the lagrangian of newtonian gravity. It does calculate the approximate metric of time correctly.
The question is then what is the role of the spatial metric? In the Einstein-Hilbert action, the spatial metric has an essential role in producing some of Ricci curvature, and contributing to the Ricci scalar. Is it possible that we could ignore the spatial metric in the lagrangian of gravity?
In our own Minkowski & newtonian gravity model, both the slowing down of time and stretching of the spatial metric are side effects of the gravity field. It does make sense to ignore the spatial metric altogether in the lagrangian!
The energy density of a gravitational wave: the inertia interaction
We empirically know that the energy density of a gravitational wave is correctly calculated by the Einstein field equations. Their energy density is 16 times the analogous electromagnetic wave. What should the lagrangian be like for gravitational waves?
Is the "kinetic" energy of the field 16X the corresponding electromagnetic lagrangian? Could that simple trick work?
Is there any reason why a "moving" field, which propagates at a speed of light, should have the same energy as a static field? In the case of electromagnetism, that holds. But for gravity, the energy is 16X. We have earlier, on December 29, 2021, estimated the energy of a gravitational wave from the work it can do against a negative pressure. We can harvest a lot of energy from the stretching of the spatial metric.
In the case of a static gravity field, it is not clear what it would mean to harvest energy from the distorted spatial metric. It might be that the energy in the distorted spatial metric is only is harvestable from a moving field.
For static fields, we can change the energy of the field simply by moving masses closer or farther from each other. The energy is manifest in the work we have to do to move the masses.
For a gravitational wave, the energy in the field is more complicated to determine. We can create gravitational waves by moving masses around. The wave can be absorbed by letting it to move masses in a receiving "antenna". The movement in the antenna cancels a part of the original wave. But how much?
oscillation
<---->
● \/\/\/\/\/\/\/\/\/ ●
M spring M
Practical gravitational waves are emitted by a quadrupole. We can have a string between two masses, and the masses oscillate until they have lost all kinetic energy into gravitational waves. The system sends quadrupole waves.
Note that the oscillation above also causes a positive and negative pressure alternating in the spring. The pressure accelerates the masses back and forth. Our December 2021 calculation with a negative pressure might not be very far from the calculation with a quadrupole.
Let us consider a rubber sheet model of gravity. We let a weight M slide back and forth on the sheet. The energy which the weight M sends in waves depends strictly on the energy in the static field of M. A wave is a part of its static field "escaping". Thus, in a rubber model, the energy of a gravitational wave probably could not be 16X the energy of the analogous electromagnetic wave. If this reasoning is correct, then a rubber model cannot explain gravity. This would be additional evidence for our claim that there is no spacetime geometry which can be bent and stretched.
A question then is what is this 16X energy density of the wave, if it is not energy density of the static field?
----> wave
... /\/\/\ ● /\/\/\ ● /\/\/\ ● /\/\/\ ...
M M M
springs and masses
If we have masses attached with springs to each other, we can send a wave along the chain. We can increase the energy of the wave by making the springs stiffer.
But if we make the springs stiffer, then we increase the strength of the attraction between the masses?
Not necessarily. If a test mass m in the field of a mass M acquires more inertia, then there is an additional interaction between m and M besides their gravity attraction – an inertia interaction. Thus, the extra inertia acquired by m can explain why the wave carries a surprisingly amount of energy.
If we let a mass M oscillate up and down in the diagram, the inertia interaction will also make the test mass m to oscillate up and down. The inertia interaction can transfer energy along surprising routes.
The inertia interaction between electric charges
This new insight may help us to determine what is the inertia of an electric test charge q in the field of an electric charge Q. We have been confused about that. We know that placing a hydrogen atom into a low or a high electric potential does not alter its spectrum, as if the electric potential would not change the inertia of the electron. On the other hand, it is hard to understand why an energy flow in the electric field would not increase the inertia of a charge.
Could it be that the energy flow only happens relatively "slowly" and does not have time to affect the inertia of the orbiting electron, or have time to affect the energy density of an electromagnetic wave?
The inertia interaction to a negative pressure: "thermal" expansion
========= very rigid structure
|| ||
=========
^
|
● M
Let us have a very rigid structure close to a mass M. We move M closer to the structure. The metric of space changes, and we can harvest energy from the deformed structure.
In what sense this was an "inertia interaction"?
In the Minkowski & newtonian model, we claim that the inertia of a test mass m is larger in the radial direction relative to M. That causes radially placed rods, relative to M, to be squeezed when they come close to M.
What is the route of energy if we push M closer to the structure, and harvest energy from the structure? Energy somehow moved from our hand to the harvesting apparatus.
rod = springs and masses
• extra inertia
| "spring"
|
... /\/\/\ ● /\/\/\ ● /\/\/\ ● /\/\/\ ...
m m m
^
|
● M
The rod might be modeled with the diagram which we drew above. The masses m are atoms which oscillate back and forth. The springs are the electromagnetic interaction. When we move the large mass M closer to the rod, the masses m gain inertia (marked with •) and move slower. Consequently, their oscillation amplitude is reduced, and the rod shrinks in length. The thermal expansion of the rod is less when it is "cooled" by bringing it closer to the large mass M.
If the rod is "cooled" by M, then where does the "heat" from the rod go? Increasing the inertia of a moving mass m releases kinetic energy from m. Could it be that the excess heat is stored into a "spring" which connects the extra inertia to m?
"Teleportation" of the cooling system
We have written about a hypothesis that waves in empty space "teleport" the transmitting antenna close to the "receiving" antenna.
Above we described how the shrinking of the length of a rod can be explained by a cooling effect by the field of M.
Gravitational waves transport the shrinking effect over large distances of space. How exactly is this transport process implemented?
We have also written about the hypothesis that a test mass m moving inside a gravitational wave ships field energy around, which would explain the increase of the inertia of m, and the cooling effect on a rod.
But the fact is that a gravitational wave is transporting 16X the energy of the analogous electromagnetic wave. This large amount of energy must be stored in the wave. Energy cannot be a "side effect" of the wave. The teleportation hypothesis can explain the large energy content. It cannot be a side effect.
The electromagnetic lagrangian: it is a rubber sheet model
A simple form is:
In the tensor notation:
Let us analyze what is the relevant part for a static electric field, and what is the part for an electromagnetic wave.
Static electric field. We will analyze the first equation above. Then the current j is zero, the vector potential A is zero, and the magnetic field B is zero. The lagrangian is essentially the lagrangian of newtonian gravity, which we analyzed above.
Electromagnetic wave. Then we have ρ = 0 and j = 0. The remaining part of the lagrangian is:
We could interpret E² as the potential energy density and B² as the kinetic energy density. The lagrangian does not directly tell us the energy density of the wave, since if an action S is at an extremal value, and C is a constant, then is also
C S
at an extremal value. The energy density of an electromagnetic wave has to be derived from its interaction with charges. The energy density happens to be:
Is it a coincidence? Why is the energy the same as for a static field? In a rubber sheet model, the energy density of the stretching of the rubber is
~ 1/2 N²,
where we have denoted by N the strain
N = ΔL / L
of the rubber sheet. The elastic energy of stretching is the same for a static field as well as for a wave. In a wave, a half of the total energy is kinetic energy. The electromagnetic formula is analogous if we identify E with the strain and B with the kinetic energy. We see that a rubber sheet model describes electromagnetism well!
Let us make a weight M oscillate back and forth on a rubber sheet. A way to describe the birth of a wave is that a part of the field of M "escapes" when M is accelerated abruptly. Then it makes sense that the energy density formula for N is the same in a static field and in a wave.
But in gravity, the energy density is a whopping 16X the energy of the analogous electromagnetic wave. Is there any way to simulate this large energy density in a rubber model?
----___ ==== bicycle chain
••••
pit
mass M
Maybe we can attach "bicycle chains" (roller chains) to the mass M. The chains have the axes of the links horizontal, so that they can effortlessly adapt to the vertical shape of the pit in the rubber sheet when the mass M is static. But if we move M rapidly back and forth on the rubber surface, then the chains transport a lot of energy away. A test mass m may be attached to one of the chains, and receives a lot of energy.
The chains implement another channel of energy transport besides the rubber sheet itself. We found an example where the static field of M contains relatively little energy, but a produced wave contains a lot of energy.
Adding a term which is linear in the stretching of the spatial metric?
The shrinking of of the metric of time pulls masses together: they can sink into a lower potential and can reduce their common potential energy.
If we, in addition, add a term which assigns a lot of energy to the stretching of the spatial metric, then we have a field which has a high energy density but only weakly pulls masses together. Then the energy density of a gravitational wave could be large, but the gravity pull weak.
This makes a lot of sense. If we make a mass M to oscillate, the bulk of the energy from the gravitational wave can be harvested from the oscillation of the spatial metric.
But how can we add the energy to the spatial stretching field? The energy cannot come from the mass M falling into a lower gravity potential. There is too little energy available there. The spatial stretching field is like a "physical body" around M. Sitting in space, not born from anything else. It is like a cloud of substance which M always carries along. That substance gets its form from the newtonian gravity field of M. How to write that into a lagrangian?
The spatial field has to be "private" for M? The field acts in a different way on the particle which creates it? How to write that into a lagrangian?
The trick is to introduce a new separate field for each particle in the universe? It is not as bad as it sounds. Every particle is, in a sense its own separate field. Add another separate field on top of that.
Conclusions
Let us close this blog post.
1. If we calculated right in April 2024, then the Einstein field equations lack a solution for a cylinder with a shear. This suggests that the Einstein equations do not have a lagrangian at all. Otherwise the minimum "energy" state of the cylinder would satisfy the Einstein equations.
2. The Einstein-Hilbert action tries to calculate the "energy" of the gravity field from the mass density alone. This cannot succeed. The action is badly incorrect. The action might work in empty space. We have to investigate.
3. The lagrangian of newtonian gravity, or the lagrangian of electromagnetism, calculates the gravity field of a mass distribution correctly, if the field is weak. Thus, it is a better lagrangian than the incorrect Einstein-Hilbert lagrangian.
4. The Einstein equations calculate the energy density of gravitational waves correctly, which is 16 times the energy density of the analogous electromagnetic wave.
A lagrangian may require that each particle has a field which acts differently on the particle creating the field from how it acts on other particles. The field is "private".