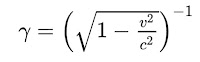Our own work in the past two months and earlier makes the concept of curved spacetime suspect – it may be impossible to describe gravity through a "metric". We thus exposed a weak point in various Big Bang models: they assume that spacetime is curved, and in addition to that, that spacetime even differs topologically from the familiar flat Minkowski space that we know.
Let us analyze these assumptions.
An interaction is expected to bend light – that does not prove that spacetime itself is curved
Bending of light when it passes the Sun is not a surprise at all. We expect gravity to pull photons. More surprising is that the bending is double the newtonian expectation. It is due to the radial metric stretching.
We have in this blog presented arguments for that the inertia, which a gravity field imposes on a test mass, explains both the slowing down of the time and the stretching of the radial metric close to a mass M. The interaction field can carry energy. One would expect that the field imposes inertia on a test mass m. It is not a surprise at all.
Why would we then assume that spacetime is curved? That is a bold and unnecessary assumption for a very mundane process of an interaction.
We have argued that the electric field expresses phenomena which are similar to gravity. Why would these phenomena in gravity be fundamentally different, so that they show that "spacetime is curved"?
Claiming that the Big Bang is the starting point of the entire universe breaks the Copernican principle
In astronomy we have observed that we live inside an explosion cloud which is expanding. The entire observable universe seems to be inside this explosion cloud.
There are explosions of various sizes in the observable universe, for example, supernova explosions.
Why should we assume that our explosion cloud is the entire universe and that the universe started from that explosion? That is an unnecessary assumption. It breaks the Copernican principle that we should not assume that we are located in a special place and time in the universe. The standard Big Bang model claims that quite a short time, only 13.7 billion years has passed since the beginning of the entire universe. We are special in the standard Big Bang model.
The Friedmann (FLRW) Big Bang model is very similar to a newtonian expansion of a dust ball. This suggests that we actually live inside an ordinary newtonian explosion. Why should we assume a topologically strange model to explain a simple newtonian explosion?
If we would be free to design the birth of a universe, why should it be so similar to an ordinary newtonian explosion? We could have a fundamentally different mechanism which creates the universe. Why pick a newtonian explosion?
Why the observable universe seems to be spatially flat?
If we use the Friedmann model, we have to fine-tune the mass-energy density of the universe at the early stage, to ensure that the spatial metric is flat after 13.7 billion years. A slight change of the density can make the universe to collapse very quickly.
People devised the inflation model to explain this fine-tuning. The inflation model is very speculative. There should be very good evidence for it before we can accept it.
A simpler explanation for the flatness might be that we live in flat Minkowski space. However, we still have to tune the explosion to be such that it does not collapse back into a black hole quickly. Maybe there is a law of nature which says that the explosion has to disperse indefinitely and it cannot collapse back?
The Milne model
We have suggested in this blog that the total gravity charge of the observable universe is zero. Then the expansion would continue at a constant speed with no deceleration.
Does this solve the flatness problem?
Currently, the mass density of the observable universe seems to be about 30% of the critical density ρc of the standard Big Bang model.
In the Milne model, the Hubble "constant" is
H = C / t,
where C is a constant and t is the time from the explosion.
How does the density of mass-energy ρ develop in the Milne model?
If a is the scale factor, the apparent energy density of photons declines as
~ 1 / a⁴,
because the observer sees arriving photons redshifted.
The energy density of massive particles declines roughly as
~ 1 / a³.
The problem becomes:
Why is the density ρ of the same order of magnitude as ρc now that 13.7 billion years has passed since the explosion? The value of ρ could be much larger or much less. It was much larger at a time t = 10 million years, and it will be much less at a time t = 1,000 billion years.
In the Milne model the spatial metric is always flat because the total gravity charge is zero. The fine-tuning is in the mass-energy density of ordinary and dark matter, relative to the critical density ρc.
Let us change the mass-energy density ρ somewhat, say, 50% from the current value. Let us then calculate backward the history of the universe. In the Milne model, the universe would have roughly the same history as we know it, but the mass-energy density would be 50% larger at every stage. The Milne model does not require a fine-tuning of the density to one part in 10⁶⁰ in the early stages, like the FLRW model does.
What evidence is there that the topology of the observable universe is as in the FLRW model?
The angular spectrum of temperature differences in the cosmic microwave background is rather "uniform", with some bumps and troughs. Supporters of the inflation hypothesis believe that inflation would create such a spectrum from "random quantum fluctuations" in a tiny primordial space.
Such random fluctuations could occur also in a newtonian explosion.
The troughs and bumps in the spectrum are explained by "baryonic oscillation" of matter soon after the Big Bang. We admit that this does support the FLRW model, though the same process might happen also in a newtonian explosion.
Conclusions
If we are able to show that a "metric" cannot describe the gravity field, then it is very unlikely that a curved spacetime like that in the FLRW model would exist. Far more probable is that the metric of spacetime is Minkowski, and the Big Bang is an ordinary, newtonian explosion. The Big Bang is not the start of the entire universe.
The Big Bang is very much like a newtonian explosion also in the FLRW model. Occam's razor implies that we should not assume the FLRW model at all, but stick to the simplest explanation: an ordinary newtonian explosion.
The Milne model removes the need for an extreme fine-tuning of the mass-energy density ρ in the early stages of the universe. Our observation is a serious blow to the Big Bang plus inflation hypothesis. The volatility of the Big Bang model is a result of the Einstein equations. The inflation hypothesis is highly speculative. We may interpret the history of modern cosmology since 1922 in this way:
1. People tried to apply to cosmology erroneous Einstein assumptions about curved spacetime.
2. They obtained the FLRW model which is extremely volatile for initial conditions. This was a sign that the model is wrong.
3. Alan Guth and others in the 1980s tried to fix the volatility problem with a very speculative inflation hypothesis.
4. It was found out that also the inflation hypothesis has to be fine-tuned to make inflation to work! Paul Steinhardt has criticized the inflation hypothesis on these grounds.
5. The expansion is not slowing down as expected. People invented a speculative cosmological constant, or dark energy, to explain this. The Milne model probably does not need dark energy to explain the astronomical observations.
This history of cosmology reminds us of the tower of turtles cosmological model: